题目内容
 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=| π | 2 |
(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求三棱锥E-AB1F的体积.
分析:(1)根据直线与平面平行的判定定理可知,只要在平面ABC里面找到一条直线与DE平行即可,过DE构造平行四边形,使其与平面ABC相交,则可得DE与交线平行,所以进一步可得DE∥平面ABC;
(2)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直去转化一下,如欲证B1F⊥AF,可以先证明AF⊥平面B1BCC1;利用勾股定理,易证明B1F⊥FE
(3)利用等体积转化,可得结论.
(2)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直去转化一下,如欲证B1F⊥AF,可以先证明AF⊥平面B1BCC1;利用勾股定理,易证明B1F⊥FE
(3)利用等体积转化,可得结论.
解答: (1)证明:设G是AB的中点,连接DG,CG,则DG平行且等于EC,…(2分)
(1)证明:设G是AB的中点,连接DG,CG,则DG平行且等于EC,…(2分)
所以四边形DECG是平行四边形,所以DE∥GC,
从而DE∥平面ABC. …(4分)
(2)证明:∵△ABC为等腰直角三角形,F为BC的中点,∴BC⊥AF,
又∵B1B⊥平面ABC,B1B?平面B1C,
∴平面ABC⊥平面B1C,
∵平面ABC∩平面B1C=BC,AF⊥BC
∴AF⊥平面B1C,
∴B1F⊥AF…(6分)
∵AB=AA1=2,∴B1F=
,EF=
,B1E=3,
∴B1F2+EF2=B1E2,∴B1F⊥FE,
∵AF∩FE=F,∴B1F⊥平面AEF…(8分)
(3)解:由题意AF=
,S△AEF=
,…(10分)
∴VE-AB1F=VB1-AEF=
S△AEF•B1F=1…(12分)
 (1)证明:设G是AB的中点,连接DG,CG,则DG平行且等于EC,…(2分)
(1)证明:设G是AB的中点,连接DG,CG,则DG平行且等于EC,…(2分)所以四边形DECG是平行四边形,所以DE∥GC,
从而DE∥平面ABC. …(4分)
(2)证明:∵△ABC为等腰直角三角形,F为BC的中点,∴BC⊥AF,
又∵B1B⊥平面ABC,B1B?平面B1C,
∴平面ABC⊥平面B1C,
∵平面ABC∩平面B1C=BC,AF⊥BC
∴AF⊥平面B1C,
∴B1F⊥AF…(6分)
∵AB=AA1=2,∴B1F=
| 6 |
| 3 |
∴B1F2+EF2=B1E2,∴B1F⊥FE,
∵AF∩FE=F,∴B1F⊥平面AEF…(8分)
(3)解:由题意AF=
| 2 |
| ||
| 2 |
∴VE-AB1F=VB1-AEF=
| 1 |
| 3 |
点评:本题主要考查空间线面关系、几何体的体积等知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.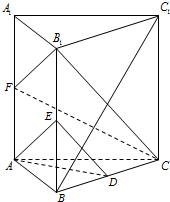 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.