题目内容
如图,在四棱锥 中,底面
中,底面 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.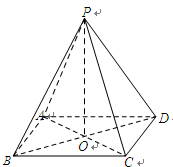
(1)求证:
 平面
平面 ;
;
(2)求证:平面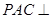 平面
平面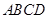 .
.
(1)根据题意,由于矩形 中,
中,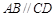 ,可以证明
,可以证明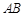
 平面
平面
(2)根据题意,由于矩形 中,点
中,点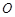 为
为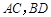 的中点,又
的中点,又 ,
,
故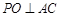 ,
,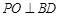 ,从而得到
,从而得到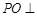 平面
平面 ,加以证明。
,加以证明。
解析试题分析:证明:(1)在矩形 中,
中,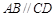 ,
,
又 平面
平面 ,
,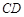
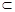 平面
平面 ,
,
所以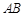
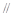 平面
平面 . ………6分
. ………6分
(2)如图,连结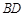 ,交
,交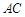 于点
于点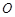 ,连结
,连结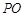 ,
,
在矩形 中,点
中,点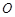 为
为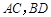 的中点,
的中点,
又 ,
,
故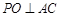 ,
,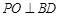 , 9分
, 9分
又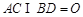 ,
,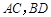
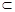 平面
平面 ,
,
所以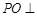 平面
平面 , 12分
, 12分
又 平面
平面 ,
,
所以平面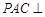 平面
平面 . 14分
. 14分
考点:线面位置关系
点评:主要是考查了线面位置关系的运用,属于中档题。

练习册系列答案
相关题目
 是矩形
是矩形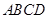 中
中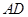 边上的点,
边上的点, 为
为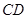 边的中点,
边的中点,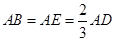 ,现将
,现将 沿
沿 边折至
边折至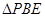 位置,且平面
位置,且平面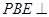 平面
平面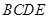 .
. 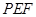 ;
;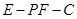 的大小.
的大小. 
 中,
中, 、
、 分别是
分别是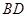 、
、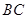 的中点,
的中点,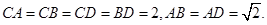
 平面
平面 ;
; 与
与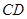 所成角余弦值的大小;
所成角余弦值的大小;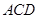 的距离.
的距离.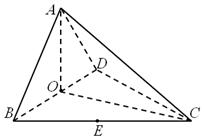
 中(图1),
中(图1),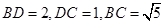 ,
,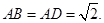
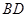 中点为
中点为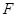 ,将图1沿直线
,将图1沿直线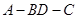 为
为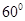 (图2)
(图2)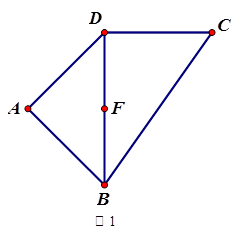
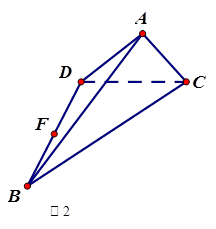
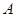 作直线
作直线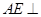 平面
平面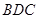 ,且
,且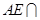 平面
平面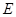 ,求
,求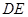 的长度。
的长度。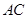 与平面
与平面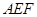 所成角的正弦值。
所成角的正弦值。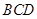 是等边三角形,
是等边三角形, 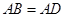 ,
,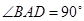 ,
,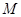 ,
, ,
,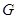 分别是
分别是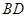 ,
,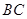 ,
, 的中点,将△
的中点,将△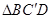 的位置,使得
的位置,使得 .
.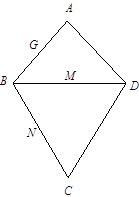

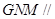 平面
平面 ;
;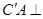 平面
平面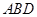 .
. 中,D,E分别是AB,BB1的中点,
中,D,E分别是AB,BB1的中点, =AC=CB=
=AC=CB= AB.
AB.
 //平面
//平面 ;
; -E的正弦值.
-E的正弦值.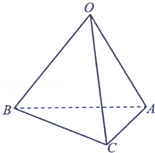
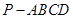 中,
中,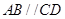 ,
,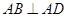 ,
,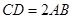 ,平面
,平面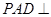 底面
底面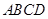 ,
,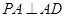 .
.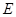 和
和 分别是
分别是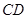 和
和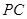 的中点,求证:
的中点,求证:
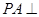 底面
底面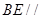 平面
平面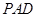 ;
;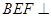 平面
平面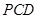 .
.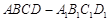 中,
中,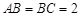 ,过
,过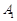 、
、 、
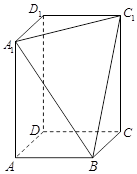
、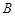 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体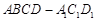 ,且这个几何体的体积为
,且这个几何体的体积为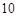 .
.
 的长;
的长;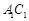 的中点为
的中点为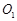 ,求异面直线
,求异面直线 与
与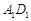 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).