题目内容
已知实数a,b,c满足a+b+c=2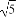
,求a2+2b2+c2的最小值.
8
【解析】由柯西不等式,得:
(a2+2b2+c2)[12+(
)2+12]≥(a+b+c)2,
∵a+b+c=2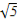
,
∴(a2+2b2+c2)·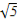
≥(2)2,
∴a2+2b2+c2≥8,
当且仅当
=
=
,
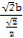即a=2b=c=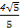
时,a2+2b2+c2取最小值8.
练习册系列答案
相关题目
题目内容
已知实数a,b,c满足a+b+c=2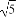,求a2+2b2+c2的最小值.
8
【解析】由柯西不等式,得:
(a2+2b2+c2)[12+()2+12]≥(a+b+c)2,
∵a+b+c=2,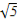
∴(a2+2b2+c2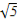)·≥(2)2,
∴a2+2b2+c2≥8,
当且仅当==,
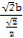即a=2b=c=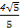时,a2+2b2+c2取最小值8.
