题目内容
设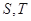 是
是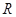 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从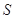 到
到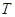 的函数
的函数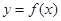 满足:(i)
满足:(i)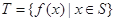 ;(ii)对任意
;(ii)对任意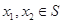 ,当
,当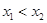 时,恒有
时,恒有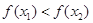 .那么称这两个集合“保序同构”.现给出以下4对集合.①
.那么称这两个集合“保序同构”.现给出以下4对集合.①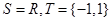 ;②
;② ;③
;③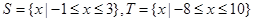 ;④
;④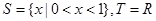 ,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
②③④.
解析试题分析:“保序同构”的集合是指存在一函数 满足:(1).S是
满足:(1).S是 的定义域,T是值域,(2).
的定义域,T是值域,(2).  在S上递增.对于①,若任意
在S上递增.对于①,若任意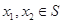 ,当
,当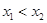 时,可能有
时,可能有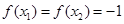 ,不是恒有
,不是恒有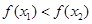 成立,所以①中的两个集合不一定是保序同构,对于②,取
成立,所以①中的两个集合不一定是保序同构,对于②,取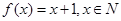 符合保序同构定义,对于③,取函数
符合保序同构定义,对于③,取函数 符合保序同构定义,对于④,取
符合保序同构定义,对于④,取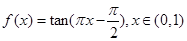 符合保序同构定义,故选②③④.
符合保序同构定义,故选②③④.
考点:新概念信息题,单调函数的概念,蕴含映射思想.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若函数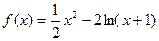 在其定义域的一个子区间
在其定义域的一个子区间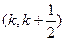 上不是单调函数,则实数
上不是单调函数,则实数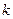 的取值范围是(***)
的取值范围是(***)
A. | B.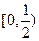 | C.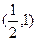 | D.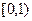 |
 的定义域为
的定义域为 ,若存在闭区间
,若存在闭区间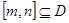 ,使得函数
,使得函数 的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)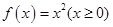
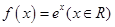
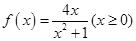
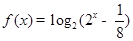
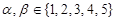 ,那么使得
,那么使得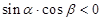 的数对
的数对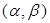 有 个.
有 个.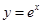 的图象与
的图象与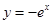 的图象关于
的图象关于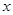 轴对称;
轴对称;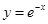 的图象关于
的图象关于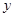 轴对称;
轴对称;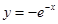 的图象关于坐标原点对称.
的图象关于坐标原点对称.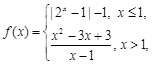 函数
函数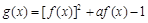 (其中a为常数),给出下列结论:
(其中a为常数),给出下列结论: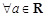 ,函数
,函数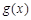 至少有一个零点;
至少有一个零点;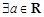 ,函数
,函数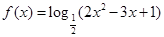 的增区间是____________.
的增区间是____________.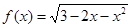 的定义域为 .
的定义域为 .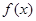 在R上存在导数
在R上存在导数 ,对任意的
,对任意的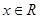 有
有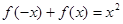 ,且在
,且在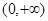 上
上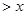 .若
.若 ,则实数
,则实数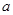 的取值范围 .
的取值范围 .