题目内容
函数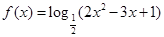 的增区间是____________.
的增区间是____________.
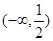
解析试题分析: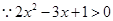 ,
,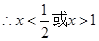 .∵二次函数
.∵二次函数 的减区间是
的减区间是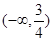 ,∴
,∴ 的增区间是
的增区间是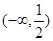 .
.
考点:复合函数的单调性.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
函数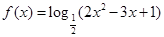 的增区间是____________.
的增区间是____________.
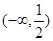
解析试题分析: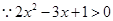 ,
,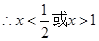 .∵二次函数
.∵二次函数 的减区间是
的减区间是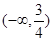 ,∴
,∴ 的增区间是
的增区间是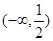 .
.
考点:复合函数的单调性.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案