题目内容
设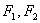 分别是椭圆的
分别是椭圆的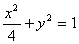 左,右焦点。
左,右焦点。
(Ⅰ)若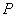 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且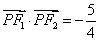 ,求点
,求点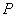 的坐标。
的坐标。
(Ⅱ)设过定点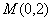 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点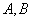 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线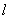 的斜率
的斜率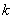 的取值范围。
的取值范围。
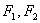 分别是椭圆的
分别是椭圆的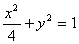 左,右焦点。
左,右焦点。(Ⅰ)若
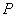 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且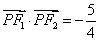 ,求点
,求点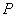 的坐标。
的坐标。(Ⅱ)设过定点
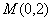 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点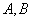 ,且
,且 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线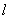 的斜率
的斜率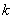 的取值范围。
的取值范围。(Ⅰ)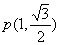 (Ⅱ)
(Ⅱ)
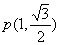 (Ⅱ)
(Ⅱ)
试题分析:(Ⅰ)易知
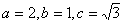 。
。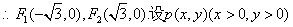
则
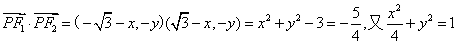 ,
,联立

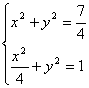 ,解得
,解得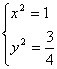
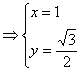 ,
,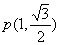
(Ⅱ)显然
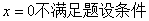 可设
可设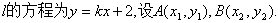
联立
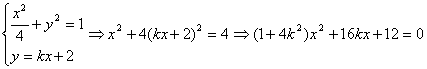
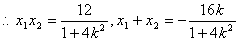
由
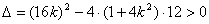
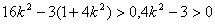 得
得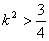 ①
①又
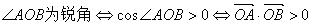 ,
,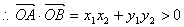 又
又
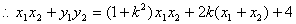
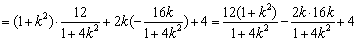
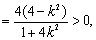
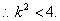 ②
②综①②可知

点评:直线与椭圆相交时常联立方程,利用韦达定理转化较简单,条件中将
 转化为向量表示,进而与A,B坐标联系起来,即可利用韦达定理
转化为向量表示,进而与A,B坐标联系起来,即可利用韦达定理
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
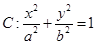 的顶点为
的顶点为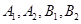 ,焦点为
,焦点为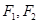 ,
,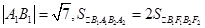 .
. 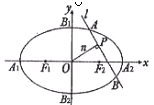
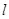 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,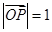 .是否存在上述直线
.是否存在上述直线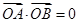 成立?若存在,求出直线
成立?若存在,求出直线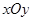 中,点
中,点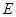 到两点
到两点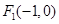 ,
,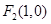 的距离之和为
的距离之和为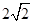 ,设点
,设点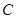 .
.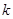 (
(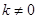 )的直线
)的直线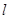 与曲线
与曲线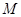 ,
,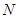 ,点
,点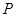 在
在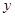 轴上,且
轴上,且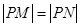 ,求点
,求点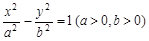 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )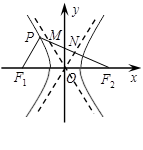

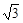

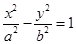 (
(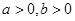 )的右焦点
)的右焦点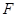 作圆
作圆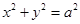 的切线
的切线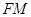 ,交
,交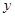 轴于点
轴于点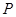 ,切圆于点
,切圆于点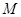 ,若
,若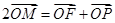 ,则双曲线的离心率是( )
,则双曲线的离心率是( )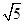
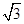
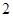
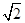
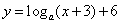 (
(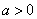 ,
,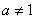 )的图象恒过定点
)的图象恒过定点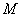 ,椭圆
,椭圆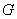 :
: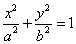 (
(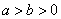 )的左,右焦点分别为
)的左,右焦点分别为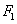 ,
,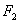 ,直线
,直线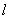 经过点
经过点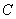 :
: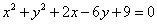 相切.
相切.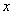 轴上方的交点为
轴上方的交点为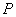 ,且
,且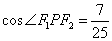 ,求
,求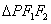 内切圆的方程.
内切圆的方程.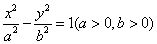 的一条渐近线方程是y=
的一条渐近线方程是y=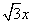 ,它的一个焦点在抛物线
,它的一个焦点在抛物线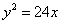 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为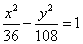
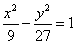

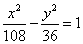
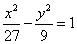
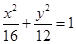 上找一点,使这一点到直线
上找一点,使这一点到直线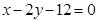 的距离为最小,并求最小值。
的距离为最小,并求最小值。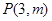 在以点
在以点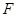 为焦点的抛物线
为焦点的抛物线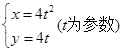 上,则
上,则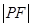 等于__________
等于__________