题目内容

已知函数f(x)=sin(ωx+
π
3
)(ω＞0)，若f(
π
6
)=f(
π
3
)且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，则ω的值为（　　）
A．
2
3
B．
5
3
C．
14
3
D．
38
3
∵f（x）=sin（ωx+
π
3
）（ω＞0），且f（
π
6
）=f（
π
3
），
在区间（
π
6
，
π
3
）上有最小值，无最大值，
∴直线x=
π
6
+
π
3
2
=
π
4
为f（x）=sin（ωx+
π
3
）（ω＞0）的一条对称轴，
∴ω•
π
4
+
π
3
=2kπ-
π
2
（k∈Z），
∴ω=4（2k-
5
6
）（k∈Z），又ω＞0，
∴当k=1时，ω=
14
3
．
故选：C．
练习册系列答案
相关题目
（本小题满分12分）
已知函数的定义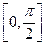域为，值域为．试求函数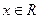（）的最小正周期和最值．
函数y=tan(2x-
π
4
)的周期是（　　）
A．πB．
π
2
C．
π
4
D．2π
如图为f（x）=Asin（ωx+ϕ）（A＞0，?＞0，ϕ∈（-π，0））的图象的一段，
（Ⅰ）求其解析式．
（Ⅱ）将f（x）图象上所有的点纵坐标不变，横坐标放大到原来的2倍，然后再将新的图象向左平移
π
2
个单位，得到函数g（x）的图象，求函数g（x）在x∈[0，
π
2
]的值域．
函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（2010）=______．
已知f（x）=sin(ωx+
π
3
)（ω＞0），f（
π
6
）=f（
π
3
），且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，则ω=______．
要得到函数y=2sin(3x-
π
5
)的图象，只需将函数y=2sin3x的图象向______．
已知
a
=（cosx，sinx），
b
=（sinx，cosx），与f（x）=
a
•
b
要得到函数y=sin4x-cos4x的图象，只需将函数y=f（x）的图象（　　）
A．向左平移
π
2
个单位长度		B．向右平移
π
2
个单位长度
C．向左平移
π
4
个单位长度		D．向右平移
π
4
个单位长度
已知向量
a
=（1+cosωx，1），b=（1，a+
3
sinx）（ω为常数且ω＞0），函数f（x）=
a
•
b
在R上的最大值为2．
（Ⅰ）求实数a的值；
（Ⅱ）把函数y=f（x）的图象向右平移
π
6ω
个单位，可得函数y=g（x）的图象，若y=g（x）在[0，
π
4
]上为增函数，求ω取最大值时的单调增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网