题目内容
20．已知x，y的取值如下表所示：| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A． | 7.35 | B． | 7.33 | C． | 7.03 | D． | 2.6 |
分析 根据表中的数据可以分别求出变量x，y的算术平均值，而根据回归方程知道直线的斜率为0.95，然后带入求截距的公式即可求出a，再求出当x=5时，$\stackrel{∧}{y}$的值．
解答 解：根据表中数据得：$\overline{x}$=2，$\overline{y}$=4.5．
又由回归方程知回归方程的斜率为0.95；
∴a=4.5-0.95×2=2.6
∴当x=5时，$\stackrel{∧}{y}$=0.95×5+2.6=7.35．
故选：A．
点评 考查线性相关的概念，回归方程中直线的斜率和截距的计算公式，以及变量的算术平均值的计算．
练习册系列答案
相关题目
5．
若函数y=sin（ωx-φ）（ω＞0，|φ|＜π）在区间$[{-\frac{π}{2}，π}]$的简图如图所示，则ω，φ的值分别是（ ）
若函数y=sin（ωx-φ）（ω＞0，|φ|＜π）在区间$[{-\frac{π}{2}，π}]$的简图如图所示，则ω，φ的值分别是（ ）| A． | $ω=2，φ=\frac{π}{3}$ | B． | $ω=2，φ=-\frac{2π}{3}$ | C． | $ω=\frac{1}{2}，φ=\frac{π}{3}$ | D． | $ω=\frac{1}{2}，φ=-\frac{2π}{3}$ |
12．
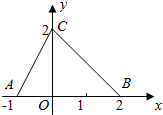如图，函数f（x）的图象为折线ACB，则不等式f（x）＞2x-1的解集是（ ）
如图，函数f（x）的图象为折线ACB，则不等式f（x）＞2x-1的解集是（ ）| A． | {x|-1＜x≤0} | B． | {x|-1≤x≤1} | C． | {x|-1≤x＜1} | D． | {x|-1＜x≤2} |