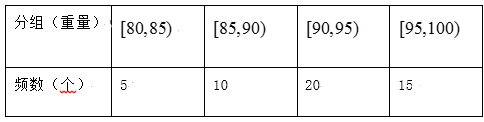
题目内容
【题目】已知![]() 是各项均为正数的无穷数列,且满足
是各项均为正数的无穷数列,且满足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求a的值;
,求a的值;
(2)设数列![]() 满足
满足![]() ,其前n项的和为
,其前n项的和为![]() .
.
①求证:![]() 是等差数列;
是等差数列;
②若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立.求证:
成立.求证:![]() .
.
【答案】(1)![]() ;(2)①证明见解析;②证明见解析.
;(2)①证明见解析;②证明见解析.
【解析】
(1)因为![]() ,所以此时
,所以此时![]() 单调递增,
单调递增,![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,解出
,解出![]() ,同理将
,同理将![]() ,
,![]() 的值代入可得出答案.
的值代入可得出答案.
(2)①由题意,![]() ,由
,由![]() ,得
,得![]() ,当
,当![]() 成立,当
成立,当![]() 时,可得
时,可得![]() 和
和![]() ,两式相减化简可得
,两式相减化简可得![]() ,从而可证明.
,从而可证明.
②由①可得![]() ,又存在
,又存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,当
,当![]() 成立,当
成立,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 必为整数,即
必为整数,即![]() ,要证
,要证![]() ,只需证即证
,只需证即证![]() ,因为
,因为![]() ,只需证明
,只需证明![]() 即可.
即可.
(1)![]() 是各项均为正数的无穷数列,
是各项均为正数的无穷数列,![]()
解:因为![]() ,所以此时
,所以此时![]() 单调递增,
单调递增,![]()
又![]()
所以令![]() ,得
,得![]() ,即
,即![]() ,
,
平方整理得![]() .
.
因为![]() ,所以
,所以![]() ;
;
同理令![]() ,得
,得![]() ,即
,即![]() ,
,
平方整理得![]() .因为
.因为![]() ,所以
,所以![]() ,因此
,因此![]() .
.
(2)证明:①由题意,![]() ,由
,由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 是公差为0的等差数列.
是公差为0的等差数列.
当![]() 时,因为
时,因为![]()
所以![]() ①,
①,
从而有![]() ②.
②.
①-②,得![]() ,
,
化简得![]() .
.
因为![]() ,且数列
,且数列![]() 的各项均为正数,
的各项均为正数,![]() ,
,
所以![]() ,从而
,从而![]() ,因此
,因此![]() .
.
因为![]() ,所以
,所以![]() .
.
综上,![]() 是公差为d的等差数列.
是公差为d的等差数列.
②因为![]() 是公差为d的等差数列,所以
是公差为d的等差数列,所以![]() .
.
因为对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
所以有![]() ,
,
整理得![]() .
.
ⅰ.若![]() ,则
,则![]() ,结论成立.
,结论成立.
ⅱ.若![]() ,
,![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 必为整数,即
必为整数,即![]() .
.
因为![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,
,
从而![]() .
.
下证![]() ,即证
,即证![]() ,
,
从而只要证![]() ,
,
因此要证![]() .
.
记![]() ,则
,则![]() .
.
记![]() ,则
,则![]() ,
,
所以![]() ,
,
从而![]() ,
,
所以![]() .
.

练习册系列答案
相关题目