题目内容
4.下函数f(x)=2sin(2x+$\frac{π}{6}$),当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时f(x)的值域为( )| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-1,1] | C. | [-$\frac{1}{2}$,1] | D. | [-1,2] |
分析 由条件利用正弦函数的定义域和值域,求得f(x)的值域.
解答 解:当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
故2sin(2x+$\frac{π}{6}$)∈[-1,2],即f(x)∈[-1,2],
故选:D.
点评 本题主要考查正弦函数的定义域和值域,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
19.设a1,a2,a3,a4∈R+,P=a${\;}_{1}^{2}$+a${\;}_{2}^{2}$+a${\;}_{3}^{2}$+a${\;}_{4}^{2}$,Q=a1a2+a2a3+a3a4+a4a1,则有( )
| A. | P<Q | B. | P>Q | C. | P≤Q | D. | P≥Q |
16.设集合∪=R,M={x||x|<2},N={y|y=2x-1},则(CUM)∪(CUN)=( )
| A. | (-1,2) | B. | (-∞,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪[2,+∞) |
13.圆C1:(x-3)2+y2=1,圆C2:(x+3)2+y2=4,若圆M与两圆均外切,则圆心M的轨迹是( )
| A. | 双曲线的一支 | B. | 一条直线 | C. | 椭圆 | D. | 双曲线 |
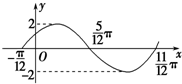 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$) 的部分图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$) 的部分图象如图所示.