题目内容
已知定义域为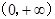 的函数
的函数 满足:(1)对任意
满足:(1)对任意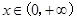 ,恒有
,恒有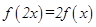 成立;(2)当
成立;(2)当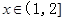 时,
时,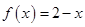 .给出如下结论:①对任意
.给出如下结论:①对任意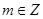 ,有
,有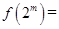
 ;②函数
;②函数 的值域为
的值域为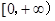 ;③存在
;③存在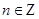 ,使得
,使得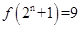 ;④“函数
;④“函数 在区间
在区间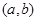 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在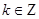 ,使得
,使得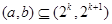 ”.其中所有正确结论的序号是 .
”.其中所有正确结论的序号是 .
①②④
解析试题分析:由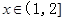 时,
时,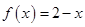 得,
得,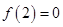 ,由任意
,由任意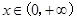 ,恒有
,恒有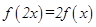 成立,取
成立,取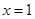 得
得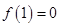 ;①任意
;①任意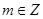 ,当
,当 时,
时, ,当
,当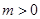 时
时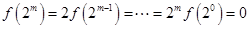 ,当
,当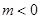 时,
时, ,故①正确;②取
,故①正确;②取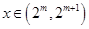 ,则
,则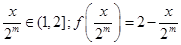 ,从而
,从而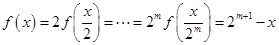 ,其中,
,其中,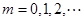 从而
从而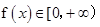 ,②正确;③由②得
,②正确;③由②得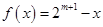 ,令
,令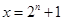 ,则有
,则有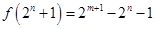 ,假设存在
,假设存在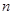 使
使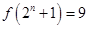 ,即存在
,即存在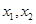 ,
,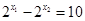 ,又
,又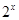 变化如下:
变化如下: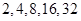 ,显然不存在,所以③错;④根据前面的
,显然不存在,所以③错;④根据前面的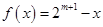 ,
,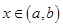 时,故
时,故 是递减的,容易知道④正确,综合可知答案为①②④
是递减的,容易知道④正确,综合可知答案为①②④
考点:抽象函数及应用.

练习册系列答案
相关题目
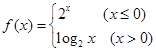 ,那么
,那么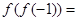 ;若
;若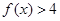 ,则
,则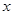 的取值范围是 .
的取值范围是 .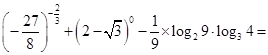 .
.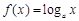 (其中
(其中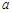 为常数且
为常数且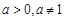 ),满足
),满足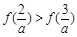 ,则
,则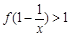 的解集是 .
的解集是 .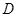 的函数
的函数 和
和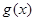 ,若存在
,若存在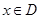 ,使得
,使得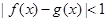 ,则
,则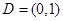 的四组函数如下:
的四组函数如下: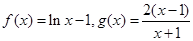 ②
②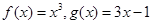
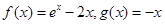 ④
④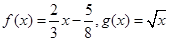
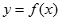 是定义在
是定义在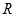 上周期为2的周期函数,且
上周期为2的周期函数,且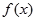 是偶函数,当
是偶函数,当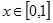 时,
时,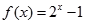 ,则函数
,则函数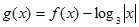 的零点个数为__________.
的零点个数为__________.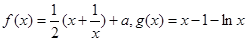 ,若存在
,若存在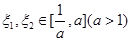 ,使得
,使得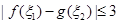 ,则
,则 的取值范围是______.
的取值范围是______.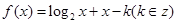 在区间(2,3)上有零点,则
在区间(2,3)上有零点,则 = .
= .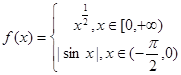 ,若
,若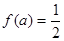 ,则
,则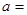 .
.