题目内容
对于具有相同定义域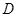 的函数
的函数 和
和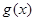 ,若存在
,若存在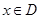 ,使得
,使得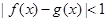 ,则
,则 和
和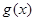 在
在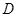 上是“亲密函数”.给出定义域均为
上是“亲密函数”.给出定义域均为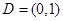 的四组函数如下:
的四组函数如下:
①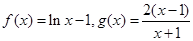 ②
②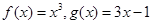
③ 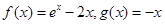 ④
④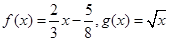
其中,函数 和
和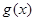 在
在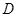 上是“亲密函数”的是 .
上是“亲密函数”的是 .
②④
解析试题分析:要使 和
和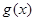 在
在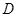 上是“密切函数”,只需
上是“密切函数”,只需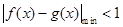 .对于①,
.对于①,
令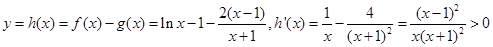 ,所以
,所以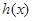 在
在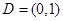 上单调递增,故其值域为
上单调递增,故其值域为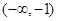 ,①不是“密切函数”;对于②,采用和①同样的方法求得
,①不是“密切函数”;对于②,采用和①同样的方法求得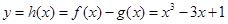 在
在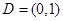 上的值域为
上的值域为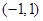 ,故②是“密切函数”;对于③,采用和①同样的方法求得
,故②是“密切函数”;对于③,采用和①同样的方法求得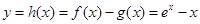 在
在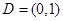 上的值域为
上的值域为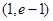 ,故③不是“密切函数”;对于④,令
,故③不是“密切函数”;对于④,令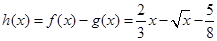 ,令
,令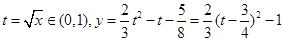 ,求得其值域为
,求得其值域为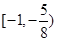 ,故④是“密切函数”,选②④.
,故④是“密切函数”,选②④.
考点:1.利用导数判断函数的单调性;2.函数值域的求法.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
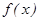 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b]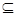 D,使得函数
D,使得函数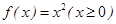 ; ②、
; ②、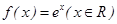 ;
;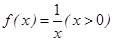 ; ④、
; ④、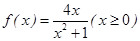 .
. 、
、 满足
满足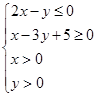 ,则
,则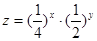 的最小值为 .
的最小值为 . 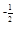 <(3-2a)
<(3-2a) (其中
(其中 为常数且
为常数且 ),满足
),满足 ,则
,则 的解集是 .
的解集是 .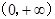 的函数
的函数 满足:(1)对任意
满足:(1)对任意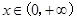 ,恒有
,恒有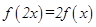 成立;(2)当
成立;(2)当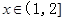 时,
时,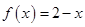 .给出如下结论:①对任意
.给出如下结论:①对任意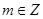 ,有
,有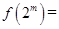
 ;②函数
;②函数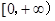 ;③存在
;③存在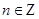 ,使得
,使得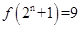 ;④“函数
;④“函数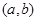 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在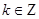 ,使得
,使得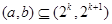 ”.其中所有正确结论的序号是 .
”.其中所有正确结论的序号是 . 在[-1,+ ∞)上是减函数,则a的取值范围是 .
在[-1,+ ∞)上是减函数,则a的取值范围是 .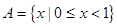 ,
,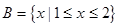 ,函数
,函数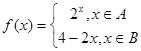 ,
,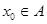 且
且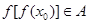 ,则
,则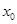 的取值范围是 .
的取值范围是 .