题目内容
给出下列四个命题：
①函数是定义域到值域的映射；
②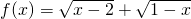
是函数；
③函数y=3x（x∈N）的图象是一条直线；
④已知函数f（x）的定义域为R，对任意实数x1，x2，且x1≠x2，都有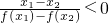
，则f（x）在R上是减函数．
其中正确命题的序号是________．（写出你认为正确的所有命题序号）
④
分析：①为假命题，函数是非空数集A到非空数集B的映射，其中A是定义域，值域是B的子集；②为假命题，函数的定义域不能为空集；③为假命题，函数y=3x（x∈N）的图象是一条直线上的孤立的点；④为真命题，对任意实数x1，x2，且x1≠x2，都有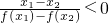，说明x1-x2与f（x1）-f（x2）异号，由单调性的定义可得结论．
解答：①为假命题，函数是非空数集A到非空数集B的映射，其中A是定义域，值域是B的子集；
②为假命题，不存在实数x同时满足两个根式有意义，函数的定义域不能为空集；
③为假命题，函数y=3x（x∈N）的图象是一条直线上的孤立的点；
④为真命题，对任意实数x1，x2，且x1≠x2，都有，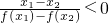
说明x1-x2与f（x1）-f（x2）异号，由单调性的定义可知f（x）在R上是减函数．
故答案为：④．
点评：本题以命题为载体，考查函数与映射的关系，考查函数的单调性，知识点多，需谨慎．
分析：①为假命题，函数是非空数集A到非空数集B的映射，其中A是定义域，值域是B的子集；②为假命题，函数的定义域不能为空集；③为假命题，函数y=3x（x∈N）的图象是一条直线上的孤立的点；④为真命题，对任意实数x1，x2，且x1≠x2，都有
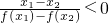，说明x1-x2与f（x1）-f（x2）异号，由单调性的定义可得结论．解答：①为假命题，函数是非空数集A到非空数集B的映射，其中A是定义域，值域是B的子集；
②为假命题，不存在实数x同时满足两个根式有意义，函数的定义域不能为空集；
③为假命题，函数y=3x（x∈N）的图象是一条直线上的孤立的点；
④为真命题，对任意实数x1，x2，且x1≠x2，都有
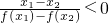，说明x1-x2与f（x1）-f（x2）异号，由单调性的定义可知f（x）在R上是减函数．
故答案为：④．
点评：本题以命题为载体，考查函数与映射的关系，考查函数的单调性，知识点多，需谨慎．
练习册系列答案
相关题目