题目内容
7. 已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°.
已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°.(1)求证:AB⊥PD;
(2)求PC与平面PAD所成的角的正弦值.
分析 (1)取AB的中点O,利用线面垂直的性质定理证明AB⊥面POD,即可证明AB⊥PD;
(2)建立空间坐标系,利用向量法即可求PC与平面PAD所成的角的正弦值.
解答  证明:(1)∵正△PAB和菱形ABCD,
证明:(1)∵正△PAB和菱形ABCD,
∴取AB的中点O,
连接PO,OD,
则PO⊥AB,AB⊥OD,
∵PO∩OD=0,
∴AB⊥面POD,
∵PD?面POD,
∴AB⊥PD;
(2)∵面PAB⊥面ABCD,PO⊥AB,
∴PO⊥面ABCD,
以O为坐标原点,OA,OD,OP分别为x,y,z轴建立空间坐标系,
设OA=1,则AB=AP=2,
即OP=$\sqrt{3}$,OD=$\sqrt{3}$,
即A(1,0,0),P(0,0,$\sqrt{3}$),D(0,$\sqrt{3}$,0),B(-1,0,0),
$\overrightarrow{AD}$=(-1,$\sqrt{3}$,0),$\overrightarrow{PA}$=(1,0,-$\sqrt{3}$,),$\overrightarrow{PD}$=(0,$\sqrt{3}$,-$\sqrt{3}$,)
$\overrightarrow{DC}$=$\overrightarrow{AB}$=(-2,0,0),
则$\overrightarrow{PC}$=$\overrightarrow{PD}$+$\overrightarrow{DC}$=(-2,$\sqrt{3}$,-$\sqrt{3}$,)
设平面PAD的法向量为$\overrightarrow{n}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PA}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x-\sqrt{3}z=0}\\{-x+\sqrt{3}y=0}\end{array}\right.$,
令x=$\sqrt{3}$,则y=z=1,
即$\overrightarrow{n}$=($\sqrt{3}$,1,1),
则PC与平面PAD所成的角的正弦值sinθ=|cos<$\overrightarrow{n}$,$\overrightarrow{PC}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{PC}|}{|\overrightarrow{n}||\overrightarrow{PC}|}$=|$\frac{-2\sqrt{3}+\sqrt{3}-\sqrt{3}}{\sqrt{5}×\sqrt{4+3+3}}$|=$\frac{2\sqrt{3}}{5\sqrt{2}}$=$\frac{\sqrt{6}}{5}$.
点评 本题主要考查线面垂直的性质的应用,以及直线和平面所成角的求解,利用向量法是解决直线和平面所成角的常用方法,考查学生的推理能力.

 阅读快车系列答案
阅读快车系列答案 如图所示,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,CE=2AF=2.
如图所示,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,CE=2AF=2. 如图(1),△ABD为等边三角形,△BCD是以C为直角顶点的等腰直角三角形且CD=2,E为线段CD中点,将△ABD沿BD折起(如图2),使得线段AC的长度等于2,对于图二,完成以下各小题:
如图(1),△ABD为等边三角形,△BCD是以C为直角顶点的等腰直角三角形且CD=2,E为线段CD中点,将△ABD沿BD折起(如图2),使得线段AC的长度等于2,对于图二,完成以下各小题: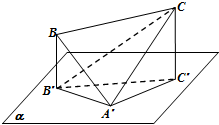 如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$. 如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.