题目内容
12. 如图(1),△ABD为等边三角形,△BCD是以C为直角顶点的等腰直角三角形且CD=2,E为线段CD中点,将△ABD沿BD折起(如图2),使得线段AC的长度等于2,对于图二,完成以下各小题:
如图(1),△ABD为等边三角形,△BCD是以C为直角顶点的等腰直角三角形且CD=2,E为线段CD中点,将△ABD沿BD折起(如图2),使得线段AC的长度等于2,对于图二,完成以下各小题:(1)证明:AC⊥平面BCD;
(2)求直线AE与平面ABD所成角的正弦值;
(3)线段AB上是否存在点P,使得平面CPE与平面ABD垂直?若存在,请求出线段BP的长度;若不存在,请说明理由.
分析 (1)根据线面垂直的判定定理即可证明:AC⊥平面BCD;
(2)建立空间坐标系,利用向量法即可求直线AE与平面ABD所成角的正弦值;
(3)根据面面垂直的判定定理,结合向量法进行证明即可.
解答 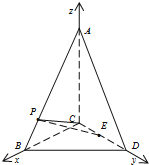 解:(1)∵$CD=CB=2,AB=BD=AD=2\sqrt{2}$
解:(1)∵$CD=CB=2,AB=BD=AD=2\sqrt{2}$
又∵AC=2,∴AC2+CB2=8=AB2
∴AC⊥CB
同理可证AC⊥CD,
故AC垂直面BCD内两条相交直线
则AC⊥平面BCD …(3分)
(2)由(1)知AC⊥CB,AC⊥CD,又有CD⊥CB
故可建如图所示建立空间直角坐标系C-xyz.…(4分)
∴C(0,0,0),A(0,0,2),B(2,0,0),D(0,2,0),E(0,1,0)
∴$\overrightarrow{AB}=(2,0,-2)$,$\overrightarrow{AD}=(0,2,-2)$,$\overrightarrow{AE}=(0,1,-2)$,$\overrightarrow{CE}=(0,1,0)$
设平面ABD的一个法向量为$\overrightarrow m=(x,y,z)$,
则$\left\{\begin{array}{l}\vec m•\overrightarrow{AB}=0\\ \vec m•\overrightarrow{AD}=0\end{array}\right.$$⇒\left\{\begin{array}{l}2x-2z=0\\ 2y-2z=0\end{array}\right.$,
取x=1,得$\overrightarrow m=(1,1,1)$.…(6分)
设直线AE与平面ABD所成角为θ,
则$sinθ=|cos<\overrightarrow m,\overrightarrow{AE}>|=\frac{{|\overrightarrow m•\overrightarrow{AE}|}}{{|\overrightarrow{{m_{\;}}}||\overrightarrow{AE}}}=\frac{1}{{\sqrt{5}×\sqrt{3}}}=\frac{{\sqrt{15}}}{15}$,…(7分)
∴设直线AE与平面ABD所成角的正弦值为$\frac{{\sqrt{15}}}{15}$.…(8分)
(3)假设存在符合条件的点P,并设$\overrightarrow{BP}=λ\overrightarrow{BA}=λ(-2,0,2)=(-2λ,0,2λ)$(λ∈[0,1])
则$\overrightarrow{CP}=\overrightarrow{CB}+\overrightarrow{BP}=(2,0,0)+(-2λ,0,2λ)=(2-2λ,0,2λ)$
设平面CPE的一个法向量为$\overrightarrow n=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=0}\\{\overrightarrow{n}•\overrightarrow{CP}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{y=0}\\{(2-2λ)x+2λz=0}\end{array}\right.$,
取x=λ,得$\overrightarrow n=(λ,0,λ-1)$.…(11分)
要使得平面CPE与平面ABD垂直,
只需$\overrightarrow m•\overrightarrow n=0$即1×λ+0×1+1×(λ-1)=0
解得$λ=\frac{1}{2}$∈[0,1],
故线段AB上存在点P,使得平面CPE与平面ABD垂直,此时线段BP的长度为$\sqrt{2}$…(14分)
点评 本题主要考查空间面面垂直和线面垂直的判断,以及直线和平面所成角的求解,利用向量法是解决空间角的基本方法.

| 2 | 4 | 8 | 14 | … |
| 6 | 10 | 16 | 24 | … |
| 12 | 18 | 26 | 36 | … |
| 20 | 28 | 38 | 50 | … |
| … | … | … | … | … |
(Ⅱ) 若aij=502,求i,j的值;(只需写出结论)
(Ⅲ)设bn=ann,cn=$\frac{1}{2^n}-\frac{4}{{{b_{n+1}}-2}}$(n∈N*,),记数列{cn}的前n项和为Sn,求Sn;并求正整数k,使得对任意n∈N*,均有Sk≥Sn.
 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,点E,F,G分别为PB,PA,BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,点E,F,G分别为PB,PA,BC的中点. 已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°.
已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°. 如图,在四棱锥PABCD中,底面ABCD是直角梯形,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
如图,在四棱锥PABCD中,底面ABCD是直角梯形,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.