题目内容
20.已知定义在(-∞,-1)∪(1,+∞)上的函数f(x)=1n$\frac{x+1}{x-1}$.(1)试判断f(x)的奇偶性;
(2)若函数在(1,4)上为增函数,解关于t的不等式f(t)+f(t-6)<0.
分析 (1)根据已知中函数f(x)=1n$\frac{x+1}{x-1}$,得到f(-x)=-f(x),可得f(x)为奇函数.
(2)结合(1)中函数的奇偶性和单调性及定义域,可解不等式.
解答 解:(1)∵f(x)=1n$\frac{x+1}{x-1}$.
∴f(-x)=ln$\frac{x-1}{x+1}$=1n($\frac{x+1}{x-1}$)-1=-1n$\frac{x+1}{x-1}$=-f(x),
则f(x)为奇函数.
(2)∵f(x)为奇函数,
∴不等式f(t)+f(t-6)<0.等价为f(t)<-f(t-6)=f(6-t).
∵函数在(1,4)上为增函数,
∴$\left\{\begin{array}{l}1<t<4\\ 1<6-t<4\\ t<6-t\end{array}\right.$,即$\left\{\begin{array}{l}1<t<4\\ 2<t<5\\ t<3\end{array}\right.$,
解得:t∈(2,3)
点评 本题考查的知识点是函数的单调性和函数的奇偶性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.探究函数$f(x)=x+\frac{4}{x},x∈(0,+∞)$的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)上递减;
函数$f(x)=x+\frac{4}{x}(x>0)$在区间[2,+∞)上递增.
当x=2时,y最小=4
(1)用定义法证明:函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)递减.
(2)思考:函数$f(x)=x+\frac{4}{x}(x<0)$时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)上递减;
函数$f(x)=x+\frac{4}{x}(x>0)$在区间[2,+∞)上递增.
当x=2时,y最小=4
(1)用定义法证明:函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)递减.
(2)思考:函数$f(x)=x+\frac{4}{x}(x<0)$时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
9.已知有三个数a=($\frac{11}{3}$)-2,b=40.3,c=80.25,则它们之间的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
10.在正方体ABCD-A1B1C1D1中,AA1=a,E,F分别是BC,DC的中点,则异面直线AD1与EF所成角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30 |
 如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.
如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.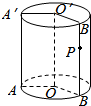 如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$. 已知如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.
已知如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.