题目内容
11. 如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.
如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.(1)求证:平面B1C1E⊥平面ACD1;
(2)证明平面B1C1E∥平面ADF,并求两个平面间的距离.
分析 (1)以A点为坐标原点,建立空间坐标系,求出平面B1C1E和平面ACD1的法向量,根据法向量垂直,可得平面B1C1E⊥平面ACD1;
(2)求出平面平面ADF的法向量,根据两个法向量平行,可得平面B1C1E∥平面ADF,代入点到直线距离公式,可得答案.
解答 证明:(1)以A点为坐标原点,建立如图所示的空间坐标系,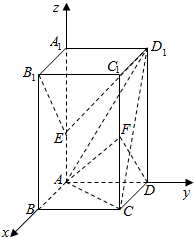
∵AB=AD=1,AA1=$\sqrt{2}$.
∴B1(1,0,$\sqrt{2}$),C1(1,1,$\sqrt{2}$),E(0,0,$\frac{\sqrt{2}}{2}$),C(1,1,0),D1(0,1,$\sqrt{2}$),
则$\overrightarrow{{B}_{1}{C}_{1}}$=(0,1,0),$\overrightarrow{{B}_{1}{E}_{\;}}$=(-1,0,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{{AD}_{1}}$=(0,1,$\sqrt{2}$),
设平面B1C1E的一个法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}\overrightarrow{{B}_{1}{C}_{1}}⊥\overrightarrow{m}\\ \overrightarrow{{B}_{1}{E}_{\;}}⊥\overrightarrow{m}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{{B}_{1}{C}_{1}}•\overrightarrow{m}=0\\ \overrightarrow{{B}_{1}{E}_{\;}}•\overrightarrow{m}=0\end{array}\right.$,即$\left\{\begin{array}{l}y=0\\-x-\frac{\sqrt{2}}{2}z=0\end{array}\right.$,
令x=1,则$\overrightarrow{m}$=(1,0,-$\sqrt{2}$),
设平面ACD1的一个法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}\overrightarrow{AC}⊥\overrightarrow{n}\\ \overrightarrow{{AD}_{1}}⊥\overrightarrow{n}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{AC}•\overrightarrow{n}=0\\ \overrightarrow{{AD}_{1}}•\overrightarrow{n}=0\end{array}\right.$,即$\left\{\begin{array}{l}x+y=0\\ y+\sqrt{2}z=0\end{array}\right.$,
令x=$\sqrt{2}$,则$\overrightarrow{n}$=($\sqrt{2}$,-$\sqrt{2}$,1),
∵$\overrightarrow{m}$•$\overrightarrow{n}$=$\sqrt{2}$-$\sqrt{2}$=0,
∴平面B1C1E⊥平面ACD1;
(2)∵D(0,1,0),F(1,1,$\frac{\sqrt{2}}{2}$),
∴$\overrightarrow{AD}$=(0,1,0),$\overrightarrow{AF}$=(1,1,$\frac{\sqrt{2}}{2}$),
设平面ADF的一个法向量$\overrightarrow{h}$=(x,y,z),
则$\left\{\begin{array}{l}\overrightarrow{AF}⊥\overrightarrow{h}\\ \overrightarrow{{AD}_{\;}}⊥\overrightarrow{h}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{AF}•\overrightarrow{h}=0\\ \overrightarrow{{AD}_{\;}}•\overrightarrow{h}=0\end{array}\right.$,即$\left\{\begin{array}{l}y=0\\ x+y+\frac{\sqrt{2}}{2}z=0\end{array}\right.$
令x=1,则$\overrightarrow{h}$=(1,0,-$\sqrt{2}$),
由$\overrightarrow{m}∥\overrightarrow{h}$,
∴平面B1C1E∥平面ADF,
又∵$\overrightarrow{AE}$=(0,0,$\frac{\sqrt{2}}{2}$),
∴两个平面间的距离d=$\frac{|\overrightarrow{AE}•\overrightarrow{m}|}{\left|\overrightarrow{AE}\right|}$=$\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}$
点评 本题考查的知识点是平面垂直的判定与平面平行的判断,平面距离的运算,建立空间坐标系,将空间线面关系,转化为空间向量关系,是解答的关键.

| A. | 2 | B. | -2 | C. | 2或-2 | D. | 不能确定 |
| A. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | B. | a3+b3≥2ab2 | C. | $\sqrt{|a-b|}≥\sqrt{a}-\sqrt{b}$ | D. | a2+b2+2≥2a+2b |
| A. | 函数f(x)=1既是奇函数又是偶函数 | B. | 函数f(x)=(1-x)$\sqrt{\frac{1+x}{1-x}}$是偶函数 | ||
| C. | 函数f(x)=$\frac{{x}^{2}-2x}{x-2}$是奇函数 | D. | 函数f(x)=x+$\sqrt{{x}^{2}-1}$是非奇非偶函数 |