题目内容
【题目】现有高一学生两人，高二学生两人，高三学生一人，将这五人排成一行，要求同一年级的学生不能相邻，则不同的排法总数为______.
【答案】48
【解析】
先求得五个人的全排列,除去相邻的情况,即为同一年级学生不相邻的情况.
将五个人全排列,共有
种;
高一学生和高二学生都相邻:捆绑法把高一两个人和高二两个人看成一个整体,再三个团体全排列,共有
种.
高一学生相邻,高二学生不相邻:捆绑法把高一学生作为一个整体排列,和高三学生再全排列,将高二的学生插3个空位中的两个,共有
种.
高二学生相邻,高一学生不相邻:捆绑法把高而学生作为一个整体排列,和高三学生再全排列,将高一的学生插3个空位中的两个,共有种.
所以满足同一年级的学生不能相邻的总排列方法有
种
故答案为:48
一本好题口算题卡系列答案【题目】广东省2021年高考将实行“
”模式，其最大特点就是取消文理科，除语文、数学、外语之外，从物理、历史这2科中自由选择一门科目；化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理（选择物理、化学、生物）的选择是否与性别有关，从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计，选择全理的人数比不选全理的人数多10人.
（1）请完成下面的
列联表：
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
（2）估计有多大把握认为选择全理与性别有关，并说明理由；
（3）现从这50名学生中已经选取了男生3名，女生2名进行座谈，从这5人中抽取2名代表作问卷调查，求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:
，其中
.
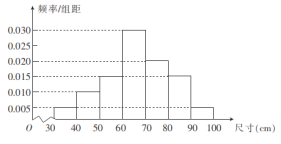
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；
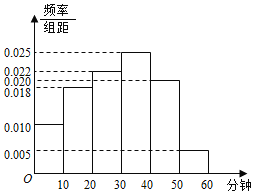
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
（1）根据已知条件完成下面的
列联表，并据此资料你是否认为“体育迷”与性别有关？
（2）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.
附：参考公式：
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）若将频率视为概率，回答下列问题：
①记甲快递公司的快递员的日工资为
（单位：元），求的分布列和数学期望；
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．