题目内容
已知函数f(x)= x
x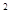 -ax+(a-1)
-ax+(a-1) ,
, 。
。
(1)讨论函数 的单调性;(2)若
的单调性;(2)若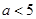 ,设
,设 ,
,
(ⅰ)求证g(x)为单调递增函数;
(ⅱ)求证对任意x ,x
,x

 ,x
,x
 x
x ,有
,有 .
.
 x
x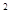 -ax+(a-1)
-ax+(a-1) ,
, 。
。(1)讨论函数
 的单调性;(2)若
的单调性;(2)若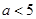 ,设
,设 ,
,(ⅰ)求证g(x)为单调递增函数;
(ⅱ)求证对任意x
 ,x
,x

 ,x
,x
 x
x ,有
,有 .
.(1)当a=2时,f(x)在(0,+∞)单调递增;
当1<a<2时,f(x)在(a-1,1)单调递减,在(0,a-1),(1,+∞)单调递增;
当a>2时,f(x)在(1,a-1)单调递减,在(0,1),(a-1,+∞)单调递增.
(2)见解析.
当1<a<2时,f(x)在(a-1,1)单调递减,在(0,a-1),(1,+∞)单调递增;
当a>2时,f(x)在(1,a-1)单调递减,在(0,1),(a-1,+∞)单调递增.
(2)见解析.
试题分析:(1)先求出函数的导函数,然后求出
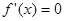 时的驻点,再由
时的驻点,再由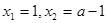 的大小关系讨论导函数的正负,从而确定函数的单调性;(2)(ⅰ)由
的大小关系讨论导函数的正负,从而确定函数的单调性;(2)(ⅰ)由 得出
得出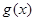
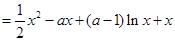 ;求出
;求出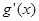 ,由
,由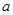 的范围得从而得出出
的范围得从而得出出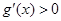 ,函数单调递增;(ⅱ)由
,函数单调递增;(ⅱ)由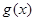 单调递增定义可推导.
单调递增定义可推导.试题解析:(1)∵函数f(x)=
 x2-ax+(a-1)lnx,其中a>1,
x2-ax+(a-1)lnx,其中a>1,∴f(x)的定义域为(0,+∞),
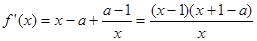
令
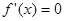 解得:
解得: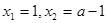 .
.①若a-1=1,即a=2时,
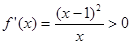
故f(x)在(0,+∞)单调递增.
②若0<a-1<1,即1<a<2时,
由f′(x)<0得,a-1<x<1;
由f′(x)>0得,0<x<a-1,或x>1.
故f(x)在(a-1,1)单调递减,在(0,a-1),(1,+∞)单调递增.
③若a-1>1,即a>2时,
由f′(x)<0得,1<x<a-1;由f′(x)>0得,0<x<1,或x>a-1.
故f(x)在(1,a-1)单调递减,在(0,1),(a-1,+∞)单调递增.
综上可得,当a=2时,f(x)在(0,+∞)单调递增;
当1<a<2时,f(x)在(a-1,1)单调递减,在(0,a-1),(1,+∞)单调递增;
当a>2时,f(x)在(1,a-1)单调递减,在(0,1),(a-1,+∞)单调递增.
(2) (ⅰ)

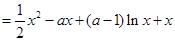
则
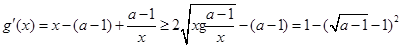 .10分
.10分由于1<a<5,故
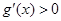 ,即g(x)在(0, +∞) 上单调递增. .11分
,即g(x)在(0, +∞) 上单调递增. .11分(ⅱ)由(ⅰ)知当
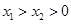 时有
时有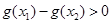 ,即
,即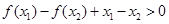 ,
,故
 ,当
,当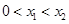 时,有
时,有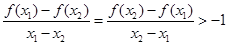 14分
14分
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 ,
, 在
在 处切线方程;
处切线方程; 上单调递减;
上单调递减; 对任意的
对任意的 都成立,求实数
都成立,求实数 的最大值.
的最大值.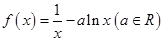 .
.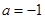 时,试确定函数
时,试确定函数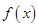 在其定义域内的单调性;
在其定义域内的单调性;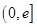 上的最小值;
上的最小值;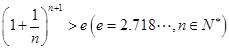 .
. .
. 的单调区间;
的单调区间; 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; (
( 是自然对数的底数)使
是自然对数的底数)使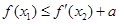 ,求实数
,求实数

 在
在 处的切线垂直
处的切线垂直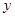 轴,求
轴,求 的值;
的值; 上为增函数,求
上为增函数,求 的单调性.
的单调性.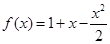
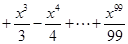 ,
,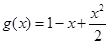
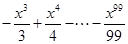 .若函数
.若函数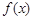 的零点为
的零点为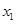 ,函数
,函数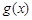 的零点为
的零点为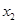 ,则有( )
,则有( )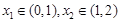
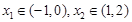
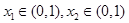
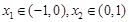
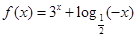 的零点所在区间为( )
的零点所在区间为( )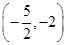
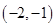

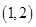
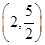
 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 =
= ,则称
,则称 是
是 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤
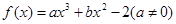 有且仅有两个不同的零点
有且仅有两个不同的零点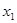 ,
,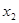 ,则( )
,则( ) 时,
时, ,
,
 ,
,
 时,
时,