题目内容
在曲线y=x3+x-1上求一点P,使过P点的切线与直线4x-y=0平行.
(1,1)或(-1,-3).
∵y′=3x2+1,根据导数的几何意义,曲线在P(x0,y0)处的切线的斜率k=y′|x=x0,
即3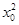 +1=4,∴x0=±1.
+1=4,∴x0=±1.
当x0=1时,y0=1,此时切线为y-1=4(x-1),即y=4x-3;当x0=-1时,y0=-3,此时切线为y+3=4(x+1),即y=4x+1.
综上可得P点坐标为(1,1)或(-1,-3).
即3
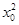 +1=4,∴x0=±1.
+1=4,∴x0=±1.当x0=1时,y0=1,此时切线为y-1=4(x-1),即y=4x-3;当x0=-1时,y0=-3,此时切线为y+3=4(x+1),即y=4x+1.
综上可得P点坐标为(1,1)或(-1,-3).

练习册系列答案
相关题目
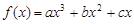 的导函数为
的导函数为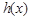 ,
,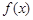 的图象在点
的图象在点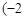 ,
,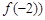 处的切线方程为
处的切线方程为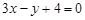 ,且
,且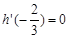 ,直线
,直线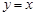 是函数
是函数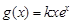 的图象的一条切线.
的图象的一条切线.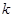 的值;
的值;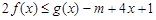 对于任意
对于任意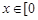 ,
,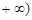 恒成立,求实数
恒成立,求实数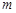 的取值范围.
的取值范围.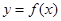 的导函数在区间
的导函数在区间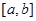 上是增函数,则函数
上是增函数,则函数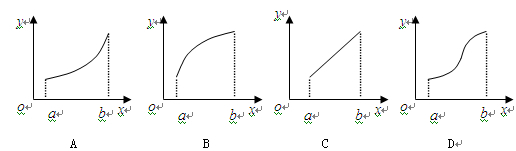
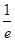
 ,则f(x)在区间[1,2],
,则f(x)在区间[1,2],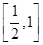 上的平均变化率分别为________.
上的平均变化率分别为________.