题目内容
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂是为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点。
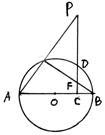
(I)求证:∠PFE=∠PAB (II)求证:CD2=CF·CP

(I)求证:∠PFE=∠PAB (II)求证:CD2=CF·CP
(1)利用平行线的性质定理来得到角相等。
(2)根据三角形的相似来得到线段的比值,即直角三角形BCF∽直角三角形PCA
得到结论。
(2)根据三角形的相似来得到线段的比值,即直角三角形BCF∽直角三角形PCA
得到结论。
试题分析:证明:(1)AB为直径,C在圆O上,BC⊥AC PC⊥AB
∠PAC=90°-∠P,∠PFC=90°-∠P
∴∠PAB=∠PFE
(2)连结AD、BD则AD⊥BD Rt△ABD中 CD2=AC·CB
直角三角形BCF∽直角三角形PCA
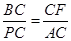
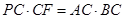
∴CD2=PC·CF
点评:主要是考查了圆内的性质以及相似三角形的性质的运用,属于基础题。

练习册系列答案
相关题目
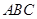 中,
中,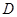 是边
是边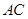 的中点,点
的中点,点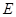 在线段
在线段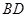 上,且满足
上,且满足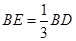 ,延长
,延长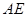 交
交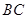 于点
于点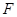 ,则
,则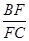 的值为 .
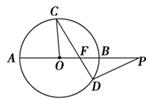
的值为 .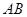 是圆
是圆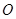 的直径,点
的直径,点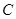 在圆
在圆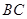 到
到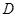 使
使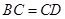 ,过
,过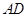 于
于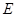 .若
.若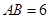 ,
,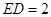 ,则
,则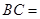 _________.
_________.
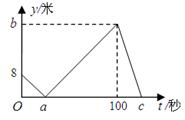
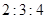 ,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).
,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).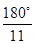
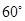
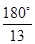
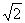 ,
,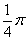 ),曲线C的参数方程为
),曲线C的参数方程为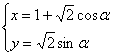 (
(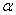 为参数),则点M到曲线C上的点的距离的最小值为 .
为参数),则点M到曲线C上的点的距离的最小值为 .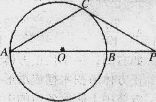
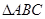 中,若
中,若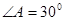 ,
,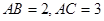 ,则
,则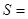
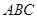 中,∠
中,∠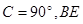 是角平分线,
是角平分线,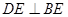 交
交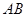 于
于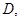 ⊙
⊙ 是△
是△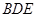 的外接圆。
的外接圆。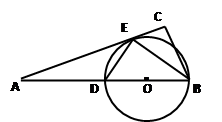
 是⊙
是⊙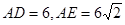 ,求
,求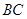 的长。
的长。