题目内容
【题目】已知函数![]() .
.
(1)若![]() 时,
时,![]() 的解集为
的解集为![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)若对任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的范围;
的范围;
(3)集合![]() ,若
,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)![]() 的解集为
的解集为![]() ,则
,则![]() ,代入即可解得b的值;
,代入即可解得b的值;
(2)存在![]() ,使
,使![]() ,则当
,则当![]() 时即可,再根据
时即可,再根据![]() 和
和![]() 分别求出b的范围,再取并集即可;
分别求出b的范围,再取并集即可;
(3)设![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,且当
,且当![]() 时,
时,![]() 无解,再根据二次函数的性质得出
无解,再根据二次函数的性质得出![]() ,代入二次函数解析式解得
,代入二次函数解析式解得![]() ,再根据
,再根据![]() 得出
得出![]() ,以及
,以及![]() 得出
得出![]() ,最终取交集得出a的取值范围.
,最终取交集得出a的取值范围.
(1)![]() 的解集为
的解集为![]() ,且
,且![]() 是二次函数,
是二次函数,
![]()
解得![]() .
.
(2)存在![]() ,使
,使![]() ,则当
,则当![]() 时即可
时即可
![]() 是开口向上的二次函数
是开口向上的二次函数
![]() 或
或![]()
①若![]()
则![]()
![]() 对任意
对任意![]() 都成立
都成立
![]() ,即
,即![]() ;
;
②若![]()
则![]()
![]() 对任意
对任意![]() 都成立
都成立
![]() ,即
,即![]() ;
;
![]() 要存在
要存在![]() ,使
,使![]()
![]() 和
和![]() 中只需一值>0即可,
中只需一值>0即可,
![]()
即实数![]() 的范围为
的范围为![]()
(3)设![]() ,
,![]() ,
,
![]()
![]() ,且当
,且当![]() 时,
时,![]() 无解
无解
![]()
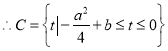
设![]() ,且
,且![]() ,
,![]()
则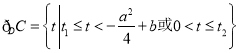 ,
,
![]()
∴当![]() 时,
时,![]() 无解
无解
若![]() ,又
,又![]()
∴当![]() 时,
时,![]() 一定有解
一定有解
![]()
又![]() ,
,![]()
![]() ,即
,即![]()
令![]() 或0
或0
![]()
又![]() 且
且![]()
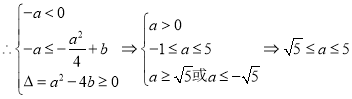
即a的取值范围为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取100名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在![]() 的男生人数有16人.
的男生人数有16人.
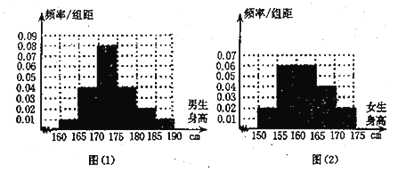
(1)试问在抽取的学生中,男,女生各有多少人?
(2)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(3)在上述100名学生中,从身高在![]() 之间的男生和身高在
之间的男生和身高在![]() 之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
参考公式:![]()
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
5.024 | 6.635 | 7.879 | 10.828 |
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
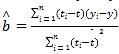 ,
,![]()