题目内容
已知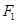 、
、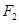 分别是椭圆
分别是椭圆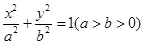 的左、右焦点,右焦点
的左、右焦点,右焦点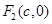 到上顶点的距离为2,若
到上顶点的距离为2,若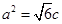 .
.
(Ⅰ)求此椭圆的方程;
(Ⅱ)点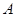 是椭圆的右顶点,直线
是椭圆的右顶点,直线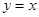 与椭圆交于
与椭圆交于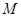 、
、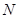 两点(
两点(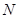 在第一象限内),又
在第一象限内),又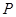 、
、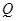 是此椭圆上两点,并且满足
是此椭圆上两点,并且满足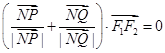 ,求证:向量
,求证:向量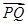 与
与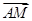 共线.
共线.
(Ⅰ)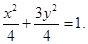 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)求此椭圆 的方程,由题意
的方程,由题意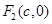 到上顶点的距离为2,即
到上顶点的距离为2,即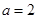 ,
,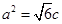 ,再由
,再由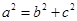 ,即可求出
,即可求出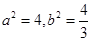 ,从而得椭圆的方程;(Ⅱ)求证:向量
,从而得椭圆的方程;(Ⅱ)求证:向量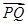 与
与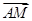 共线,即证
共线,即证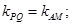 ,由于点
,由于点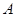 是椭圆的右顶点,可得
是椭圆的右顶点,可得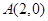 ,直线
,直线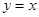 与椭圆交于
与椭圆交于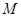 、
、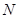 两点(
两点(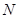 在第一象限内),可由
在第一象限内),可由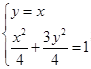 ,解得
,解得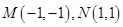 ,得
,得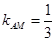 ,只需求出直线
,只需求出直线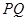 的斜率,由题意
的斜率,由题意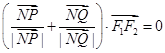 ,而
,而 与
与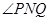 的平分线平行,可得
的平分线平行,可得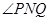 的平分线垂直于
的平分线垂直于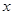 轴,设
轴,设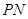 的斜率为
的斜率为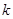 ,则
,则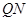 的斜率
的斜率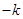 ;因此
;因此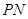 和
和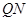 的方程分别为:
的方程分别为:
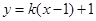 、
、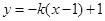 ;其中
;其中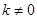 ;分别代入椭圆方程,得
;分别代入椭圆方程,得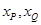 的表达式,从而可得直线
的表达式,从而可得直线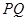 的斜率,从而可证.
的斜率,从而可证.
试题解析:(Ⅰ)由题知: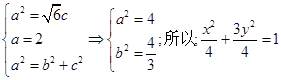
(Ⅱ)因为: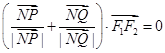 ,从而
,从而 与
与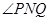 的平分线平行,
的平分线平行,
所以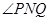 的平分线垂直于
的平分线垂直于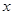 轴;
轴;
由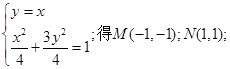 不妨设
不妨设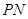 的斜率为
的斜率为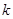 ,则
,则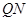 的斜率
的斜率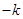 ;因此
;因此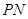 和
和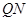 的方程分别为:
的方程分别为:
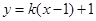 、
、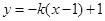 ;其中
;其中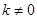 ; 由
; 由 得;
得;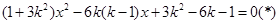 ,因为
,因为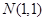 在椭圆上;所以
在椭圆上;所以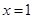 是方程
是方程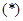 的一个根;
的一个根;
从而;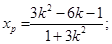 同理:
同理: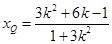 ;得
;得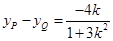 ,
,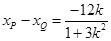
从而直线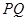 的斜率
的斜率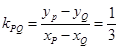 ;又
;又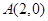 、
、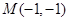 ;所以
;所以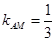 ;所以
;所以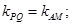 所以向量
所以向量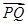 与
与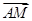 共线.
共线.
考点:椭圆方程,直线与椭圆位置关系.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
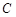 :
: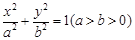 的离心率为
的离心率为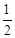 ,右焦点为
,右焦点为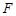 ,右顶点
,右顶点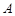 在圆
在圆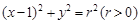 上.
上. 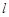 与椭圆
与椭圆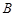 ,与圆
,与圆 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线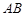 的中点,若存在,求出直线
的中点,若存在,求出直线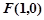 ,点
,点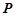 是点
是点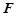 关于
关于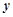 轴的对称点,过点
轴的对称点,过点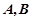 两点。
两点。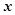 轴上是否存在不同于点
轴上是否存在不同于点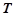 ,使得
,使得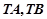 与
与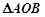 的面积为
的面积为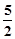 ,求向量
,求向量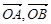 的夹角;
的夹角;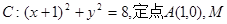 为圆上一动点,点
为圆上一动点,点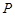 是线段
是线段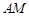 的垂直平分线与直线
的垂直平分线与直线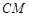 的交点.
的交点.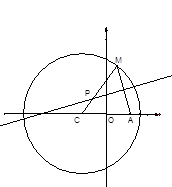
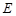 的方程;
的方程; 是曲线
是曲线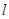 的方程;(不要求证明)
的方程;(不要求证明)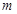 过切点
过切点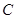 关于直线
关于直线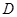 ,证明:直线
,证明:直线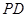 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.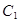 上任意一点
上任意一点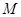 到直线
到直线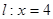 的距离是它到点
的距离是它到点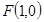 距离的
距离的 倍;曲线
倍;曲线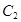 是以原点为顶点,
是以原点为顶点,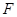 为焦点的抛物线.
为焦点的抛物线.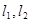 ,其中
,其中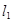 与
与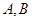 ,
,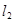 与
与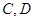 ,求四边形
,求四边形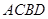 面积的取值范围.
面积的取值范围.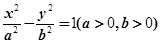 ,
,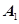 、
、 是双曲线的左右顶点,
是双曲线的左右顶点,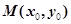 是双曲线上除两顶点外的一点,直线
是双曲线上除两顶点外的一点,直线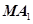 与直线
与直线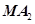 的斜率之积是
的斜率之积是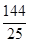 ,
,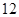 ,求双曲线的方程.
,求双曲线的方程.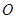 为坐标原点,如果一个椭圆经过点P(3,
为坐标原点,如果一个椭圆经过点P(3,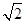 ),且以点F(2,0)为它的一个焦点.
),且以点F(2,0)为它的一个焦点.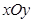 中,点
中,点 为动点,
为动点,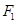 、
、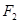 分别为椭圆
分别为椭圆 的左、右焦点.已知
的左、右焦点.已知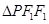 为等腰三角形.
为等腰三角形.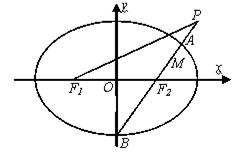
 ;
;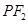 与椭圆相交于
与椭圆相交于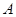 、
、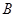 两点,
两点,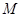 是直线
是直线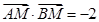 ,求点
,求点