题目内容
已知直线l1：2x－y＋a＝0(a>0)，直线l2：－4x＋2y＋1＝0和直线l3：x＋y－1＝0，且l1与l2的距离是
.
(1)求a的值；
(2)能否找到一点P，使得P点同时满足下列三个条件：①P是第一象限的点；②P点到l1的距离是P点到l2的距离的
；③P点到l1的距离与P点到l3的距离之比是
∶；若能，求P点坐标；若不能，说明理由．
解：(1)直线l2：2x－y－＝0.
所以l1与l2的距离d＝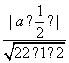
＝
，
所以
＝
所以|a＋|＝
.
因为a>0，所以a＝3.
(2)假设存在点P，设点P(x0，y0)，若P点满足条件②，则P点在与l1、l2平行的直线l′：2x－y＋C＝0上，
且
＝
，即C＝
，或C＝
，
所以2x0－y0＋＝0，或2x0－y0＋＝0；
若P点满足条件③，由点到直线的距离公式，
有
＝
，
即|2x0－y0＋3|＝|x0＋y0－1|，
所以x0－2y0＋4＝0或3x0＋2＝0；
由于P在第一象限，所以3x0＋2＝0不可能．
联立方程2x0－y0＋＝0和x0－2y0＋4＝0，
解得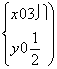
应舍去．
由
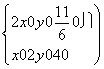解得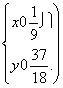
∴存在点P(
，
)同时满足三个条件．
练习册系列答案
相关题目
已知直线l1：2x-my+1=0与l2：x+（m-1）y-1=0，则“m=2”是“l1⊥l2”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
如图，直线L过点P（0，1），夹在两已知直线l1：2x+y-8=0和l2：x-3y+10=0之间的线段AB恰被点P平分．