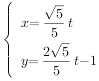题目内容
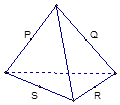
【题目】如图:在四棱锥V﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 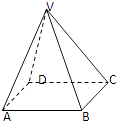
(1)求二面角V﹣AB﹣C的平面角的大小;
(2)求四棱锥V﹣ABCD的体积.
【答案】
(1)解:取AB的中点M,CD的中点N,连MN、VM、VN,
∵底面ABCD是边长为2的正方形,∴MN⊥AB,MN=2
又∵VA=VB= ![]() ,M为AB的中点,∴VM⊥AB
,M为AB的中点,∴VM⊥AB
∴∠VMN是二面角V﹣AB﹣C的平面角
在Rt△VAM中,AM=1,VA= ![]() ,
,
∴VM= ![]() =2,同理可得VN=2
=2,同理可得VN=2
∴△VMN是正三角形,可得∠VMN=60°
即二面角V﹣AB﹣C的大小为60°
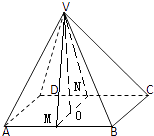
(2)解:由(1)知AB⊥平面VMN
∵AB平面ABCD,∴平面ABCD⊥平面VMN
过V作VO⊥MN于点O,
∵平面ABCD⊥平面VMN,平面ABCD∩平面VMN=MN,VO平面VMN
∴VO⊥平面ABCD,得VO是四棱锥V﹣ABCD的高
∵VM=MN=NV=2,∴VO= ![]()
因此,四棱锥V﹣ABCD的体积为
V= ![]() SABCD×VO=
SABCD×VO= ![]() =
= ![]()
【解析】(1)取AB的中点M,CD的中点N,连MN、VM、VN.利用正方形的性质和等腰三角形的“三线合一”,证出MN⊥AB且VM⊥AB,得到∠VMN是二面角V﹣AB﹣C的平面角.再根据题中数据算出△VMN是正三角形,得∠VMN=60°,即得二面角V﹣AB﹣C的大小;(2)过V作VO⊥MN于点O,利用面面垂直的性质与判定证出VO⊥平面ABCD,得VO是四棱锥V﹣ABCD的高.正三角形△VMN中算出VO的长,结合锥体的体积公式和题中的数据,即可得到四棱锥V﹣ABCD的体积.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目