题目内容
【题目】数列{an}中,a1=1,Sn表示前n项和,且Sn , Sn+1 , 2S1成等差数列.
(1)计算S1 , S2 , S3的值;
(2)根据以上结果猜测Sn的表达式,并用数学归纳法证明你的猜想.
【答案】
(1)解:S1=a1=1,由已知有2S2=S1+2S2,得S2= ![]() ,
,
又2S3=S2+2S2,得S3= ![]()
(2)解:由以上结果猜测:Sn= ![]()
② 当n=1时,S1= ![]() =1,猜想成立
=1,猜想成立
②假设当n=k时猜想成立,则有Sk= ![]()
当n=k+1时,∵2Sk+1=Sk+2S1,
∴Sk+1= ![]() +2=
+2= ![]() ,
,
∴S= ![]() ,
,
∴n=k+1时猜想成立,
故由①和②,可知猜想成立
【解析】(1)Sn , Sn+1 , 2S1成等差数列,得到2Sn+1=Sn+Sn+1 , 可求S1 , S2 , S3的值;(2)由(1)猜想Sn的表达式,再根据数学归纳法的证题步骤进行证明.
【考点精析】本题主要考查了数学归纳法的定义的相关知识点,需要掌握数学归纳法是证明关于正整数n的命题的一种方法才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】靖国神社是日本军国主义的象征.中国人民珍爱和平,所以要坚决反对日本军国主义. 2013年12月26日日本首相安倍晋三悍然参拜靖国神社,此举在世界各国激起舆论的批评.某报的环球舆情调查中心对中国大陆七个代表性城市的1000个普通民众展开民意调查. 某城市调查体统计结果如下表:
性别 中国政府是否 需要在钓鱼岛和其他争议 问题上持续对日强硬 | 男 | 女 |
需要 | 50 | 250 |
不需要 | 100 | 150 |
(1) 试估计这七个代表性城市的普通民众中,认为 “中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众所占比例;
(2) 能否有![]() 以上的把握认为这七个代表性城市的普通民众的民意与性别有关?
以上的把握认为这七个代表性城市的普通民众的民意与性别有关?
(3) 从被调查认为“中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众中,采用分层抽样的方式抽取6人做进一步的问卷调查,然后在这6人中用简单随机抽样方法抽取2人进行电视专访,记被抽到的2人中女性的人数为![]() ,求
,求![]() 的分布列.
的分布列.
附: 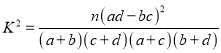
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |