题目内容
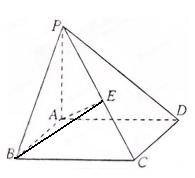
如图,三棱锥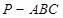 中,
中,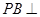 底面
底面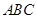 ,
,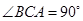 ,
,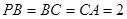 ,
,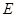 为
为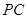 的中点,点
的中点,点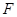 在
在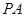 上,且
上,且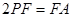 .
.
(Ⅰ)求证:平面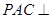 平面
平面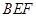 ;
;
(Ⅱ)求平面 与平面
与平面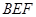 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
(Ⅰ)详见解析;(Ⅱ)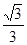 ;
;
解析试题分析:(Ⅰ)主要利用线线垂直、线面垂直可证面面垂直;(Ⅱ)通过作平行线转化到三角形内解角;当然也可建系利用空间向量来解.
试题解析:(Ⅰ)∵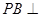 底面
底面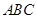 ,且
,且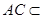 底面
底面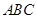 , ∴
, ∴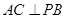 1分
1分
由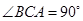 ,可得
,可得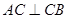 2分
2分
又∵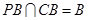 ,∴
,∴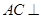 平面
平面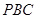
注意到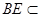 平面
平面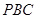 , ∴
, ∴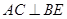 3分
3分
∵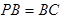 ,
,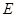 为
为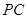 中点,∴
中点,∴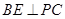 4分
4分
∵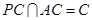 ,
, 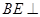 平面
平面 5分
5分
而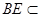 平面
平面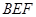 ,∴
,∴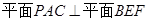 6分
6分
(Ⅱ)如图,以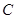 为原点、
为原点、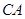 所在直线为
所在直线为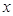 轴、
轴、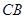 为
为 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则 8分
8分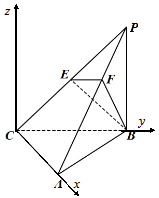
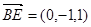
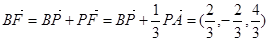 10分
10分
设平面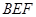 的法向量
的法向量 .
.
则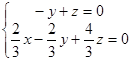
解得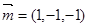 12分
12分
取平面 的法向量为
的法向量为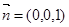 则
则 ,
,
故平面 与平面
与平面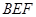 所成的二面角的平面角(锐角)的余弦值为
所成的二面角的平面角(锐角)的余弦值为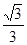 . 14分
. 14分
考点:立体几何面面垂直的证明;二面角.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
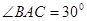 ,
,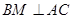 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
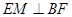 ;
;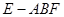 的体积
的体积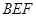 和平面
和平面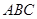 所成的锐二面角的正切值.
所成的锐二面角的正切值. 的底面
的底面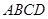 是平行四边形,且
是平行四边形,且 ,
,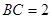 ,
,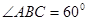 ,
, 为
为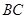 的中点,
的中点,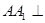 平面
平面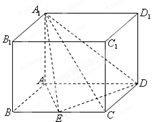
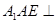 平面
平面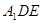 ;
;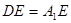 ,试求异面直线
,试求异面直线 与
与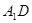 所成角的余弦值;
所成角的余弦值;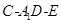 的余弦值.
的余弦值.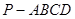 中,底面
中,底面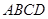 是矩形,
是矩形,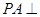 底面
底面 是
是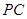 的中点,已知
的中点,已知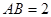 ,
,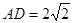 ,
,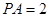 ,
,
 的面积;(II)三棱锥
的面积;(II)三棱锥 的体积
的体积 中,侧棱
中,侧棱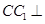 底面
底面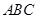 ,
,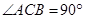 ,
,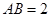 ,
,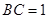 ,
,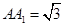 .
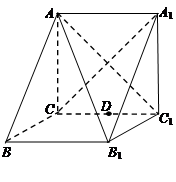
.
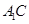
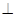 平面
平面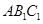 ;
;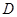 是棱
是棱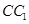 的中点,在棱
的中点,在棱 上是否存在一点
上是否存在一点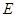 ,使
,使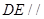 平面
平面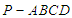 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为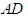 的中点。
的中点。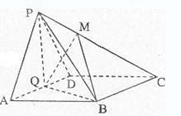
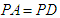 ,求证:平面
,求证:平面 ;
;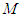 在线段
在线段 上,
上,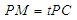 ,试确定
,试确定 的值,使
的值,使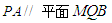 ;
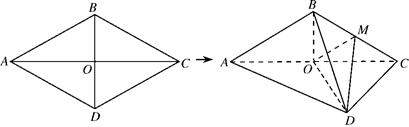
;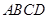 的边长为4,
的边长为4,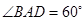 ,
,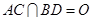 .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点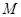 是棱
是棱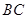 的中点,
的中点, .
.
 平面
平面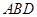 ;
;
 平面
平面 ;
; 的体积.
的体积.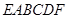 的底面
的底面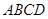 是边长为
是边长为 的正方形,
的正方形,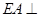 底面
底面 ,且
,且 .
. 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
 所在的平面与正方形
所在的平面与正方形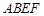 所在的平面相互垂直,
所在的平面相互垂直,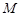 、
、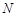 分别是
分别是 、
、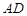 的中点.
的中点.
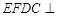 面
面 ;
; 与平面
与平面 所成的角正弦值.
所成的角正弦值.