题目内容
已知命题p:x2-x-2≤0,命题q:x2-x-m2-m≤0.
(1)若?p为真,求x的取值范围;
(2)若?q是?p的充分不必要条件,求m的取值范围.
(1)若?p为真,求x的取值范围;
(2)若?q是?p的充分不必要条件,求m的取值范围.
(1)∵p:x2-x-2≤0,∴¬p:x2-x-2>0,解得x>2或x<-1,
若?p为真,则x的取值范围是x>2或x<-1.
(2)由x2-x-2≤0得-1≤x≤2,即p:-1≤x≤2.设A={x|-1≤x≤2}
由x2-x-m2-m≤0得(x+m)[x-(m+1)]≤0,设B={x|(x+m)[x-(m+1)]≤0}
若?q是?p的充分不必要条件,即p是q的充分不必要条件.
即p⇒q成立,但q⇒p不成立,即A?B,
①若-m=m+1,即m=-
,此时B={
},不满足条件.
②若-m>m+1,即m<-
,此时B={x|m+1≤x≤-m},要使A?B,
则
,即
,即m≤-2,当m=-2时,A=B不满足条件,
∴m<-2.
③若-m<m+1,即m>-
,此时B={x|-m≤x≤m+1},要使A?B,
则
,即
,即m≥1,当m=1时,A=B不满足条件,
∴m>1.
综上m的取值范围是m>1或m<-2.
若?p为真,则x的取值范围是x>2或x<-1.
(2)由x2-x-2≤0得-1≤x≤2,即p:-1≤x≤2.设A={x|-1≤x≤2}
由x2-x-m2-m≤0得(x+m)[x-(m+1)]≤0,设B={x|(x+m)[x-(m+1)]≤0}
若?q是?p的充分不必要条件,即p是q的充分不必要条件.
即p⇒q成立,但q⇒p不成立,即A?B,
①若-m=m+1,即m=-
| 1 |
| 2 |
| 1 |
| 2 |
②若-m>m+1,即m<-
| 1 |
| 2 |
则
|
|
∴m<-2.
③若-m<m+1,即m>-
| 1 |
| 2 |
则
|
|
∴m>1.
综上m的取值范围是m>1或m<-2.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
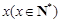 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为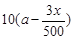 万元
万元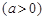 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高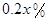 .
.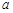 的取值范围是多少?
的取值范围是多少?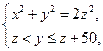 的正整数解组
的正整数解组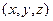 的个数.
的个数.