题目内容
若命题“?x0∈R，使得x02+mx0+2m-3＜0”为假命题，则实数m的取值范围是（ ）
| A．[2，6] | B．[-6，-2] | C．（2，6） | D．（-6，-2） |
命题“?x0∈R，使得
+mx0+2m-3＜0”的否定为：
“?x0∈R，都有
+mx0+2m-3≥0”，
由于命题“?x0∈R，使得
+mx0+2m-3＜0”为假命题，
则其否定为：“?x0∈R，都有
+mx0+2m-3≥0”，为真命题，
∴△=m2-4（2m-3）≤0，解得2≤m≤6．
则实数m的取值范围是[2，6]．
故选A．
| x | 20 |
“?x0∈R，都有
| x | 20 |
由于命题“?x0∈R，使得
| x | 20 |
则其否定为：“?x0∈R，都有
| x | 20 |
∴△=m2-4（2m-3）≤0，解得2≤m≤6．
则实数m的取值范围是[2，6]．
故选A．
练习册系列答案
备战中考寒假系列答案
相关题目
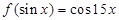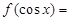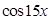
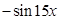
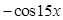
，则
( )
，则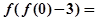
；