Question

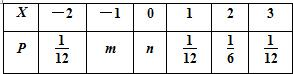已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=

1

6

，则m，n的值分别为（　　）

• A、

  1

  12

  ，

  1

  2

• B、

  1

  6

  ，

  1

  6

• C、

  1

  4

  ，

  1

  3

• D、

  1

  3

  ，

  1

  4

Answer 1

分析：由题意知根据分布列的概率之和是1，写出关于m和n的等式，根据期望是

1

6

，得到关于m和n的方差，解关于m和n的方程组，得到m和n的值．

解答：解：∵由p₁+p₂+…+p₆=1与E（X）=

1

6

∴

1

12

+m+n+

1

12

+

1

6

+

1

12

=1
-2×

1

12

+(-1)m+0+1×

1

12

+2×

1

6

+3×

1

12

=

1

6

∴

m+n= 7 12 1 2 - m= 1 6

∴m=

1

3

，n=

1

4

．
故选D

点评：本题考查离散型随机变量的分布列和期望，主要考查分布列和期望的简单应用，通过解方程组得到要求的变量，这与求变量的期望是一个相反的过程，但是两者都要用到期望的公式．