题目内容
如图，正三棱柱ABC—A1B1C1的各棱长都相等，D、E分别是CC1和AB1的中点，点F在BC上且满足BF∶FC=1∶3
(1)若M为AB中点，求证
BB1∥平面EFM；
(2)求证 EF⊥BC；
(3)求二面角A1—B1D—C1的大小
(1)若M为AB中点，求证
BB1∥平面EFM；(2)求证
EF⊥BC；(3)求二面角A1—B1D—C1的大小
(1)证明连结EM、MF，∵M、E分别是正三棱柱的棱AB和AB1的中点，
∴BB1∥ME，又BB1
平面EFM，∴BB1∥平面EFM
(2)证明 取BC的中点N，连结AN由正三棱柱得 AN⊥BC，
又BF∶FC=1∶3，∴F是BN的中点，故MF∥AN，
∴MF⊥BC，而BC⊥BB1，BB1∥ME
∴ME⊥BC，由于MF∩ME=M，∴BC⊥平面EFM，
又EF
平面EFM，∴BC⊥EF
(3)解 取B1C1的中点O，连结A1O知，A1O⊥面BCC1B1，由点O作B1D的垂线OQ，垂足为Q，连结A1Q，由三垂线定理，A1Q⊥B1D，故∠A1QD为二面角A1—B1D—C的平面角，易得∠A1QO=arctan
连结EM、MF，∵M、E分别是正三棱柱的棱AB和AB1的中点，∴BB1∥ME，又BB1
平面EFM，∴BB1∥平面EFM (2)证明
取BC的中点N，连结AN由正三棱柱得 AN⊥BC，又BF∶FC=1∶3，∴F是BN的中点，故MF∥AN，
∴MF⊥BC，而BC⊥BB1，BB1∥ME
∴ME⊥BC，由于MF∩ME=M，∴BC⊥平面EFM，
又EF
平面EFM，∴BC⊥EF (3)解
取B1C1的中点O，连结A1O知，A1O⊥面BCC1B1，由点O作B1D的垂线OQ，垂足为Q，连结A1Q，由三垂线定理，A1Q⊥B1D，故∠A1QD为二面角A1—B1D—C的平面角，易得∠A1QO=arctan 见详解
练习册系列答案
相关题目
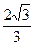为半径作一个球，则球面与正方体的表面相交所得到的曲线的长等于 。
，棱长为
的正六棱柱的所有顶点都在一个平面上，则此球的体积为 ．
中，
上是否存在一个点P，使得直线
与平面
所成角的正切值为
；（Ⅱ）若P是侧棱
上是否存在一个定点
，使得
在平面
上的射影垂直于