题目内容
已知数列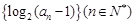 为等差数列,且
为等差数列,且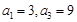 .
.
(1)求数列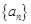 的通项公式;
的通项公式;
(2)证明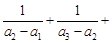 …
…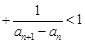 .
.
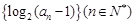 为等差数列,且
为等差数列,且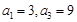 .
.(1)求数列
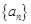 的通项公式;
的通项公式;(2)证明
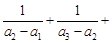 …
…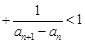 .
.(1)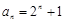 ;(2)详见解析.
;(2)详见解析.
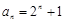 ;(2)详见解析.
;(2)详见解析.试题分析:(1)求数列
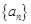 的通项公式,因为数列
的通项公式,因为数列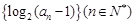 为等差数列,设公差为
为等差数列,设公差为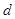 ,由
,由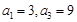 得
得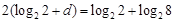 即
即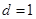 ,可写出数列
,可写出数列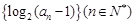 的通项公式,从而可得数列
的通项公式,从而可得数列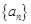 的通项公式;(2)证明
的通项公式;(2)证明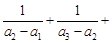 …
…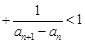 ,关键是求数列
,关键是求数列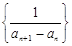 的通项公式,由(1)知
的通项公式,由(1)知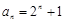 ,得
,得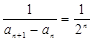 ,这样数列
,这样数列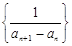 是一个以
是一个以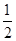 为首项,以
为首项,以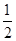 为公比的等比数列,由等比数列的前
为公比的等比数列,由等比数列的前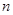 项和公式,求出和即可证出.
项和公式,求出和即可证出.试题解析:(1)设等差数列的公差为d,
由
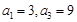 得
得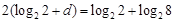 即d=1; 3分
即d=1; 3分所以
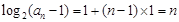 即
即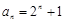 . 6分
. 6分(2)证明:
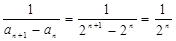 8分
8分所以
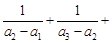
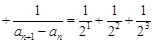
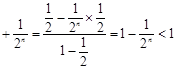 12分
12分
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
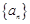 中,
中,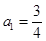 ,
,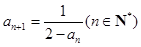 .
.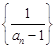 是等差数列,并求
是等差数列,并求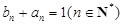 ,
,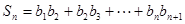 ,试比较
,试比较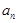 与
与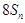 的大小.
的大小.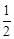 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.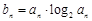 ,求数列{bn}的前n项和
,求数列{bn}的前n项和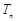 .
.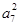 +2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )
+2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )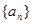 中,若
中,若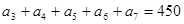 ,则数列
,则数列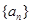 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且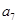 是
是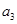 与
与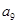 的等比中项,
的等比中项,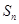 为
为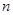 项和,
项和,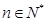 则
则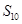 的值为( )
的值为( )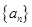 满足:公差
满足:公差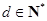 ,
,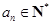 ,且
,且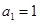 ,则
,则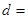 ; 若
; 若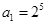 ,则
,则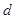 的所有可能取值之和为 .
的所有可能取值之和为 .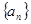 满足
满足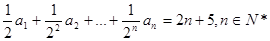 ,则
,则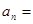 .
.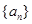 的前
的前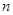 项和为
项和为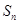 ,且
,且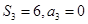 ,则公差
,则公差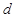 等于( )
等于( )


