题目内容
将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )
| A.26,16,8 | B.25,17,8 | C.25,16,9 | D.24,17,9 |
B
解析试题分析:依据系统抽样的规律可知抽取的各数依次构成等差数列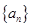 ,
,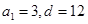
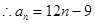
令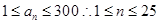 ,
,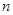 有25个值;令
有25个值;令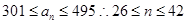 ,
,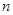 有17个值;令
有17个值;令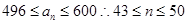
考点:系统抽样
点评:系统抽样所得样本的显著特点是样本数据间相差间隔的整数倍,因此只需确定第一组抽取的样本,其余各组就依次确定下来

练习册系列答案
相关题目
若样本 +2,
+2, +2, ,
+2, , +2的平均数为10,方差为3,则样本2
+2的平均数为10,方差为3,则样本2 +3,2
+3,2 +3,… ,2
+3,… ,2 +3,
+3,
的平均数、方差、标准差是( )
A.19,12, | B.23,12, | C.23,18, | D.19,18, |
下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
B.线性回归方程对应的直线 = = x+ x+ 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中, 为0.98的模型比 为0.98的模型比 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |
在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;
②收集数据 [
[
③求线性回归方程;
④求相关系数;
⑤根据所搜集的数据绘制散点图.
若根据实际情况能够判定变量x、y具有线性相关性,则在下列操作顺序中正确的是
| A.①②⑤③④ | B.③②④⑤① | C.②④③①⑤ | D.②⑤④③① |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线Z是由这些样本点通过 最小二乘法得到的线性回归方程(如图),以下结论中正确的是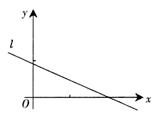
| A.x;和y正相关 |
| B.y和y的相关系数为直线I的斜率 |
| C.x和y的相关系数在-1到O之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
某中学从已编号(1~60)的60个班级中,随机抽取6个班级进行卫生检查,用每部分选取的号码间隔一样的系统抽样方法确定所选的6个班级的编号可能是( )
| A.6,16,26,36,46,56 | B.3,10,17,24,31,38 |
| C.4,11,18,25,32,39 | D.5,14,23,32,41,50 |
在如图所示的“茎叶图”表示的数据中,众数和中位数分别是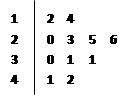
| A.23与26 | B.31与26 |
| C.24与30 | D.26与30 |
在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的 ,且样本容量为200,则第8组的频数为( )
,且样本容量为200,则第8组的频数为( )
| A.40 | B.0.2 | C.50 | D.0.25 |
 =bx+a必过( )
=bx+a必过( ) B.点
B.点 C.点
C.点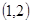 D.点
D.点