题目内容
若样本
+2，
+2， ，
+2的平均数为10，方差为3，则样本2
+3，2
+3，… ，2
+3，
的平均数、方差、标准差是（ ）
A．19，12， | B．23，12， | C．23，18， | D．19，18， |
A
解析试题分析：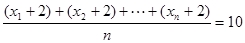
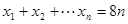
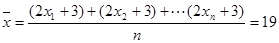
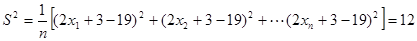,所以S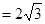
考点:算术平均数；方差；标准差．
点评:本题考查了平均数、方差和标准差的定义，方差反映了一组数据的波动大小，方差越大，波动性越
大，反之也成立．标准差是方差的算术平方根．
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案现有60件产品，编号从1到60，若用系统抽样方法从中抽取6件检验，则所抽到的个体编号可能是
| A．5，10，15，20，25，30 | B．2，14，26，28，42，56 |
| C．5，8，31，36，48，54 | D．3，13，23，33，43，53 |
一批灯泡400只，其中20 W、40 W、60 W的数目之比为4∶3∶1，现用分层抽样的方法产生一个容量为40的样本，三种灯泡依次抽取的个数为（ ）
| A．20 ,10 , 10 | B．15 , 20 , 5 | C．20, 5, 15 | D．20, 15, 5 |
为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生，得到学生视力频率分布直方图，如右图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频率成等差数列．设最大频率为a；视力在4．6到5．0之间的学生人数为b，则a、b的值分别为
| A．0.27，78 | B．0.27，83 |
| C．2.7，78 | D．2.7，83 |
下列选项中，两个变量具有相关关系的是( )
| A．正方形的面积与周长 | B．匀速行驶车辆的行驶路程与时间 |
| C．人的身高与体重 | D．人的身高与视力 |
在独立性检验中，统计量
有两个临界值：3.841和6.635；当＞3.841时，有95%的把握说明两个事件有关，当＞6.635时，有99%的把握说明两个事件有关，当
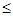3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的=20.87，根据这一数据分析，认为打鼾与患心脏病之间
| A．有95%的把握认为两者有关 | B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 | D．约有99%的打鼾者患心脏病 |
将参加夏令营的600名学生编号为：001,002，…，600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003.这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数依次为( )
| A．26,16,8 | B．25,17,8 | C．25,16,9 | D．24,17,9 |
对某商店一个月内(按30天计)每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是（ ）
| A．47,45,56 | B．46,45,53 |
| C．46,45,56 | D．45,47,53 |