在如图所示的“茎叶图表示的数据中.众数和中位数分别是A．23与26B．31与26C．24与30D．26与30 题目和参考答案——青夏教育精英家教网—

题目内容

在如图所示的“茎叶图”表示的数据中，众数和中位数分别是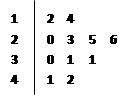

A．23与26	B．31与26
C．24与30	D．26与30

解析试题分析：根据茎叶图把数按照从小到大排列起来为12、14、20、23、25、26、30、31、31、41、42，故众数为31，中位数为26，故选B
考点：本题考查了茎叶图的运用
点评：读懂茎叶图并且理解众数及中位数的概念是解决此类问题的关键，当中间有两个数时，中位数是这两个数的平均数

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

相关题目

为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生，得到学生视力频率分布直方图，如右图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频率成等差数列．设最大频率为a；视力在4．6到5．0之间的学生人数为b，则a、b的值分别为

A．0.27，78	B．0.27，83
C．2.7，78	D．2.7，83

将参加夏令营的600名学生编号为：001,002，…，600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003.这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数依次为(　　)

已知某产品的广告费用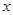万元与销售额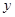万元的统计数据如表所示：

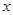（万元）	0	1	3	4
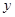（万元）	2.2	4.3	4.8	6.7

从散点图分析，

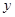与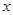

线性相关，且

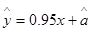，则据此模型预报广告费用为6万元时销售额为
A. 2.6万元 B. 8.3万元 C. 7.3万元 D. 9.3万元

下列命题正确的有
①用相关指数来刻画回归效果，越小，说明模型的拟合效果越好；
②命题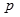：“”的否定：“”；
③设随机变量服从正态分布, 若，则；
④回归直线一定过样本中心（）.

某产品的广告费用x与销售额y的统计数据如下表：

广告费用x（万元）	4	2	3	5
销售额y（万元）	49	26	39	54

据上表得回归方程

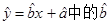为9.4，据此预报广告费用为6万元时销售额约为（）
A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元

对某商店一个月内(按30天计)每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是（）

A．47,45,56	B．46,45,53
C．46,45,56	D．45,47,53

某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒; …… 第六组，成绩大于等于18秒且小于等于19秒. 右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒的学生人数占全班总人数的百分比为, 成绩大于等于15秒且小于17秒的学生人数为，则从频率分布直方图中可分析出和分别为（）

A．0.9，35	B．0.9，45
C．0.1，35	D．0.1，45

某台机床加工的100只产品中次品数的频率分布如下表：

次品数	0	1	2	3	4
频率	0.05	0.2	0.5	0.2	0.05

则次品数的众数、中位数、平均数依次为 ( )
A.4，2，2
B.2，1.5，1
C.2, 2, 1
D.2, 2, 2

试题分类