��Ŀ����
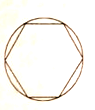
����Ŀ������Բ������������ͻ������ѧ�ɾ�֮һ�����ڡ���������ע���������Բ��������Ϊ����Բ���ܳ�������Ѿ�Բ���ʵĻ��������հ�Բ�ڽ�������ε����һֱ�㵽����3072���Σ����ɴ˶������Բ����Ϊ3.1415��3.1416������������ֵ���������ǵ�ʱ������Բ���ʼ�����ȷ����.��ͼ�����ָԲ�ڽ���������ʱ��ijͬѧ���ü�������ģ�ⷨ��Բ�����Ͷ���㣬����ó��õ��������������ڵ�Ƶ��Ϊ0.8269����ôͨ����ʵ����������Բ���ʽ���ֵΪ���ο����ݣ�![]() ��
��
A. 3.1419B. 3.1417C. 3.1415D. 3.1413
���𰸡�A
��������
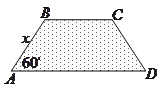
����Բ�İ뾶Ϊ![]() ����ʾ��Բ��������������ε���������������������ʣ����ɵó����.
����ʾ��Բ��������������ε���������������������ʣ����ɵó����.
��Բ�İ뾶Ϊ![]() ����Բ�����Ϊ
����Բ�����Ϊ![]() ���������ε����Ϊ
���������ε����Ϊ![]() ����������ʵ��ĸ���Ϊ
����������ʵ��ĸ���Ϊ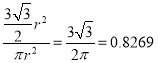 ����
����![]() .
.
��ѡA

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ijѧУΪ���˽����ѧ����������������������ȡ��40��ѧ����һ�ܵ���������ʱ�䳤����λ��Сʱ������ͳ�ƣ����������������£�
ʱ�䳤 �Ա� |
|
|
|
|
|
�� | 1 | 2 | 3 | 6 | 8 |
Ů | 0 | 2 | 10 | 6 | 2 |
��1������������������ķ�ʽ���Թ��Ƹ�У������ѧ����һ�ܵ���������ʱ�䳤Ϊ![]() �ĸ��ʣ�
�ĸ��ʣ�
��2������һ�ܵ���������ʱ�䳤������3Сʱ������Ϊ�����������ϸ�����������Ϊ�����ϸ���������������������������![]() �����������ݴ��ж��ܷ���95%�İ�����Ϊ�����������Ա��йأ�����
�����������ݴ��ж��ܷ���95%�İ�����Ϊ�����������Ա��йأ�����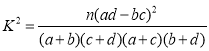 ������
������![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
����Ŀ������һ��������ҵ��Ϊ�˽�Լ�ɱ�������������죬�ֽ�ij�ֲ�Ʒ����![]() �뵥λ�ɱ�
�뵥λ�ɱ�![]() ͳ���������£�
ͳ���������£�
�·� | 1 | 2 | 3 | 4 | 5 | 6 |
������ǧ���� | 2 | 3 | 4 | 5 | 4 | 5 |
��λ�ɱ���Ԫ/���� | 73 | 72 | 71 | 73 | 69 | 68 |
������ȷ���ع鷽��![]() ��
��
����ָ������ÿ����1000��ʱ����λ�ɱ�ƽ���½����٣�
���ٶ���λ�ɱ�Ϊ70Ԫ/��ʱ������ӦΪ���ټ���
���ο���ʽ��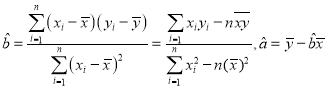 .��
.��
�������![]()
![]() ��
��