题目内容
【题目】在平面直角坐标系![]() 中已知椭圆
中已知椭圆![]() 过点
过点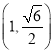 ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆E的方程;
(2)若A,B分别为椭圆E的左、右顶点,动点M满足![]() ,且MA交椭圆E于点P.
,且MA交椭圆E于点P.
(i)求证:![]() 为定值;
为定值;
(ii)设PB与以PM为直径的圆的另一交点为Q,问:直线MQ是否过定点,并说明理由.
【答案】(1) ![]() (2) (i)证明见解析,定值为4 (ii)直线
(2) (i)证明见解析,定值为4 (ii)直线![]() 过定点
过定点![]() .
.
【解析】
(1)由题意得离心率公式和点满足的方程,结合椭圆的![]() 的关系,可得
的关系,可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)(i)设![]()
![]() ,求得直线MA的方程,代入椭圆方程,解得点P的坐标,再由向量的数量积的坐标表示,计算即可得证;
,求得直线MA的方程,代入椭圆方程,解得点P的坐标,再由向量的数量积的坐标表示,计算即可得证;
(ii)直线MQ过定点O(0,0).先求得PB的斜率,再由圆的性质可得MQ⊥PB,求出MQ的斜率,再求直线MQ的方程,即可得到定点.
解:(1)易得 且
且![]() ,
,
解得
所以椭圆E的方程为![]()
(2)设![]()
![]() ,
,
①易得直线![]() 的方程为:
的方程为:![]() ,
,
代入椭圆![]() 得,
得,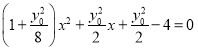 ,
,
由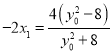 得,
得,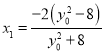 ,从而
,从而![]() ,
,
所以示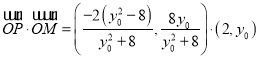
 ,
,
②直线![]() 过定点
过定点![]() ,理由如下:
,理由如下:
依题意,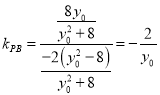 ,
,
由![]() 得,
得,![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ,
,
所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目