Question

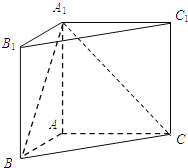
【题目】在直三棱柱中，，且异面直线与所成的角等于，设.

（1）求的值；

（2）求直线到平面的距离.

Answer 1

【答案】(1)；(2)

【解析】

（1）∠A1BC是异面直线A1B与B1C1所成的角，即∠A1BC＝60°，根据线段的长度关系可得：△A1BC为等边三角形，即可得到，进而达到a＝1．

（2）由B1C1∥平面A1BC，得点D到平面A1BC的距离等于点B1到平面A1BC的距离．再根据 求B1到平面A1BC的距离，分别求出两个三角形的面积即可．

（1）∵BC∥B1C1，∴∠A1BC就是异面直线A1B与B1C1所成的角，

即∠A1BC＝60°，又连接A1C，AB＝AC，则A1B＝A1C，∴△A1BC为等边三角形，

由AB＝AC＝1，∠BAC＝90°，∴，∴．

（2）易知B1C1∥平面A1BC，此时有B1C1上的任意一点到平面A1BC的距离等于点B1到平面A1BC的距离．

设其为d，连接B1C，由求d，又∵CA⊥A1A，CA⊥AB，

∴CA⊥平面A1B1C，并且AC＝1，．因为△A1B1B的面积，并且△A1BC的面积，

所以，即 ，所以B1C1到平面A1BC的距离等于．