题目内容
已知函数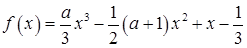 (
(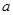
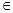 R).
R).
(1) 若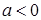 ,求函数
,求函数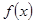 的极值;
的极值;
(2)是否存在实数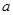 使得函数
使得函数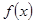 在区间
在区间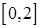 上有两个零点,若存在,求出
上有两个零点,若存在,求出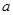 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
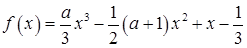 (
(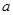
 R).
R).(1) 若
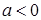 ,求函数
,求函数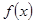 的极值;
的极值;(2)是否存在实数
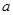 使得函数
使得函数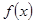 在区间
在区间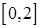 上有两个零点,若存在,求出
上有两个零点,若存在,求出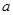 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(1)  ,
,
(2)
 ,
,
(2)

试题分析:(1)
 2分
2分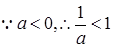 ,
,| |  | 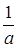 | 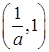 | 1 |  |
 | - | 0 | + | 0 | - |
 | 递减 | 极小值 | 递增 | 极大值 | 递减 |
 ,
, 6分
6分(2)
 ,
,
 ,
,  8分
8分① 当
 时,
时, 在
在 上为增函数,在
上为增函数,在 上为减函数,
上为减函数, ,
, ,
,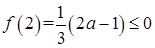 ,所以
,所以 在区间
在区间 ,
, 上各有一个零点,即在
上各有一个零点,即在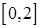 上有两个零点; 10分
上有两个零点; 10分②当
 时,
时, 在
在 上为增函数,在
上为增函数,在 上为减函数,
上为减函数, 上为增函数,
上为增函数, ,
, ,
, ,
, ,所以
,所以 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在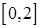 上只有一个零点; 12分
上只有一个零点; 12分③ 当
 时,
时, 在
在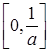 上为增函数,在
上为增函数,在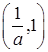 上为减函数,
上为减函数, 上为增函数,
上为增函数, ,
, ,
, ,
, , 所以
, 所以 只在区间
只在区间 上有一个零点,故在
上有一个零点,故在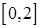 上只有一个零点; 13分
上只有一个零点; 13分故存在实数
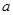 ,当
,当 时,函数
时,函数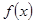 在区间
在区间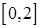 上有两个零点14分
上有两个零点14分点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.

练习册系列答案
相关题目
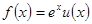 ,
,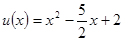 ,求函数
,求函数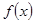 的极小值,
的极小值,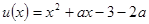 ,设
,设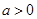 ,函数
,函数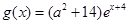 .若存在
.若存在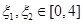 使得
使得 成立,求
成立,求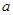 的取值范围.
的取值范围. 元(
元( 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价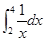 等于( )
等于( )  ,其中
,其中 的单位是米,
的单位是米, 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )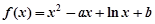
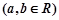 ,
,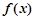 在
在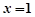 处的切线方程为
处的切线方程为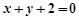 ,求实数
,求实数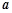 ,
,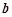 的值;
的值;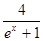 在点(0,2)处的切线方程为_______.
在点(0,2)处的切线方程为_______.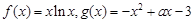 .
.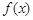 在
在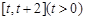 上的最小值;
上的最小值;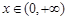 ,
,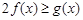 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.