题目内容
10. 已知函数f(x)=2cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx.
已知函数f(x)=2cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx.(1)求函数f(x)的单调递增区间;
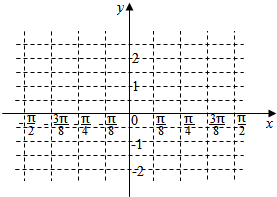
(2)在给出的直角坐标系中,画出函数f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
分析 (1)利用两角和公式和二倍角公式对函数解析式进行化简整理求得函数的解析式,进而根据正弦函数的单调性求得单调增区间;
(2)利用左加右减,上加下减的原则,将函数y=sinx纵坐标不变,横坐标缩小到$\frac{1}{2}$倍得到y=sin2x,再向左平移$\frac{π}{6}$个单位得到函数y=sin(2x+$\frac{π}{3}$),横坐标不变,纵坐标扩大2倍得到y=2sin(2x+$\frac{π}{3}$),即可得出结论.
解答 解:(1)f(x)=2cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=2cosx(sinxcos$\frac{π}{3}$+cosxsin$\frac{π}{3}$)-$\sqrt{3}$sin2x+$\frac{1}{2}$sin2x
=2sin(2x+$\frac{π}{3}$),
当2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$时,即kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{5π}{12}$,函数单调增,
∴函数的单调增区间为:[kπ-$\frac{5π}{12}$,kπ+$\frac{5π}{12}$](k∈Z).
(2)由函数y=sinx纵坐标不变,横坐标缩小到$\frac{1}{2}$倍得到y=sin2x,再向左平移$\frac{π}{6}$个单位得到函数y=sin(2x+$\frac{π}{3}$),横坐标不变,纵坐标扩大2倍得到y=2sin(2x+$\frac{π}{3}$),
点评 本题主要考查了三角函数的基本性质和三角函数的图象变换.考查了学生对基础知识点综合运用.

练习册系列答案
相关题目
15.若方程x2+y2-2x-4y+m=0表示圆,则m的取值范围是( )
| A. | m≥5 | B. | m≤5 | C. | m>5 | D. | m<5 |
2.某超市要将甲、乙两种大小不同的袋装大米分装成A,B两种规格的小袋,每袋大米可同时分得A,B两种规格的小袋大米的袋数如下表所示:
已知库房中现有甲、乙两种袋装大米的数量分别为5袋和10袋,市场急需A,B两种规格的成品数分别为15袋和27袋.
(Ⅰ)问分甲、乙两种袋装大米各多少袋可得到所需A,B两种规格的成品数,且使所用的甲、乙两种袋装大米的袋数最少?(要求画出可行域)
(Ⅱ)若在可行域的整点中任意取出一解,求其恰好为最优解的概率.
| 规格类型 袋装大米类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
(Ⅰ)问分甲、乙两种袋装大米各多少袋可得到所需A,B两种规格的成品数,且使所用的甲、乙两种袋装大米的袋数最少?(要求画出可行域)
(Ⅱ)若在可行域的整点中任意取出一解,求其恰好为最优解的概率.