题目内容
17.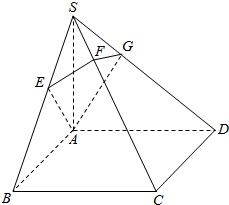 求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:
求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:(1)AE⊥SB;
(2)GE⊥平面SAC.
分析 (1)由SA⊥BC,BC⊥AB,可证BC⊥平面SAB,即得BC⊥AE,由SC⊥AE可证AE⊥平面SBC,即可证明AE⊥SB;
(2)由(1)AE⊥平面SBC,AE⊥EF,同理可证AG⊥GF,证明AF⊥GE.又可证SC⊥EG.从而得证.
解答 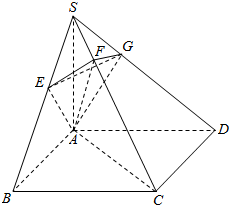 证明:(1)∵SA⊥平面ABCD,
证明:(1)∵SA⊥平面ABCD,
∴SA⊥BC,
又∵BC⊥BA,
∴BC⊥平面SAB,
∴BC⊥AE,
又∵SC⊥截面AEFG,
∴SC⊥AE,
∴AE⊥平面SBC
∴AE⊥SB;
(2)由(1)AE⊥平面SBC,AE⊥EF,
同理可证AG⊥GF,
∴A,E,F,G四点在以AF为直径的圆上,
∵△SAB≌△SAD,AE和AG都是RT三角形斜边的高,
∴AE=AG,
又∵AF=AF,∠AGF=∠AEF=90°,
∴△AEF≌△AGF,
∴AF是角平分线,即AF是等腰△AGE的高.
∴GE⊥AF.
又∵SC⊥平面AEFG.
∴SC⊥EG.
∵AF∩SC=F
∴GE⊥平面SAC.
点评 本小题主要考查空间线面关系,直线与平面垂直的判定,空间中直线与直线之间的位置关系,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,属于中档题.

练习册系列答案
相关题目
9.已知等比数列{an}前n项和为Sn,则下列一定成立的是( )
| A. | 若a7>0,则a2015<0 | B. | 若a4>0,则a2014<0 | ||
| C. | 若a7>0,则S2015>0 | D. | 若a4>0,则S2014>0 |
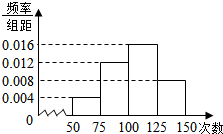 为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.
为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.