题目内容
5.F1、F2是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,直线l:y=2x+5与椭圆C交于P1,P2,已知椭圆中心O关于直线l的对称点恰好落在椭圆C的左准线上,且|P2F2|-|P1F1|=$\frac{10a}{9}$,则椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.分析 求出椭圆C的中心关于直线l的对称点的坐标,即可求椭圆C的左准线方程,得到$-\frac{{a}^{2}}{c}=-4$,再把y=2x+5代入椭圆方程,利用韦达定理,结合|P2F2|-|P1F1|=$\frac{10a}{9}$,求出a,b,c的另一等式,再结合隐含条件即可求椭圆C的方程.
解答 解:设对称点为(x,y),则$\left\{\begin{array}{l}{2•\frac{y}{x}=-1}\\{\frac{y}{2}=2•\frac{x}{2}+5}\end{array}\right.$,解得x=-4,y=2,
∴椭圆C的左准线方程为x=-4,即$-\frac{{a}^{2}}{c}=-4$ ①.
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=2x+5}\end{array}\right.$,得(4a2+b2)x2+20a2x+25a2-a2b2=0.
设P1(x1,y1),P2(x2,y2),
则x1+x2=-$\frac{20{a}^{2}}{4{a}^{2}+{b}^{2}}$,
由焦半径公式可得:|P2F2|=a-ex2,|P1F1|=a+ex1,
∴|P2F2|-|P1F1|=a-ex2-a-ex1=-e(x1+x2)=$-\frac{c}{a}•(-\frac{20{a}^{2}}{4{a}^{2}+{b}^{2}})$=$\frac{10a}{9}$ ②.
又a2=b2+c2 ③.
联立①②③解得:a2=8,b2=4.
∴椭圆C的方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
故答案为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,训练了椭圆焦半径公式的应用,考查学生的计算能力,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | [3,+∞) | B. | (-∞,3] | C. | [-3,+∞) | D. | (-∞,-3] |
| A. | -$\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | $\frac{4}{5}$ |
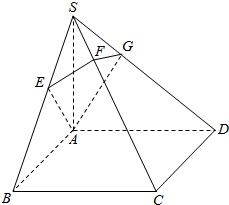 求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:
求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证: