题目内容
8.求函数y=sin2x•cosx的最大值.分析 设cosx=t,则 函数y=t-t3,t∈[-1,1].再利用导数求得函数的极值,求出函数的端点值,综合可得函数的在闭区间上的最大值.
解答 解:y=sin2x•cosx=(1-cos2x)cosx=cosx-cos3x,设cosx=t,则 函数y=t-t3,t∈[-1,1].
令y′=1-3t2=0,求得t=±$\frac{\sqrt{3}}{3}$,在(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)上,y′>0,函数y为增函数;
在(-1,-$\frac{\sqrt{3}}{3}$)、($\frac{\sqrt{3}}{3}$,1]上,y′<0,函数y为减函数,
故函数的极大值为f($\frac{\sqrt{3}}{3}$)=$\frac{2\sqrt{3}}{9}$,极小值为f(-$\frac{\sqrt{3}}{3}$)=-$\frac{2\sqrt{3}}{9}$,
再根据f(-1)=0,f(1)=0,可得函数y=t-t3在[-1 1]上的最大值为f($\frac{\sqrt{3}}{3}$)=$\frac{2\sqrt{3}}{9}$.
点评 本题主要考查同角三角函数的基本关系,利用导数求函数的极值,求函数在闭区间上的最值,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
19.已知角θ的顶点在原点,始边与x轴的正半轴重合,终边在直线2x-3y=0上,则tan2θ=( )
| A. | $\frac{12}{13}$ | B. | $\frac{12}{5}$或-$\frac{12}{5}$ | C. | $\frac{12}{5}$ | D. | -$\frac{12}{5}$或$\frac{12}{13}$ |
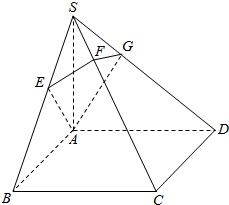 求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:
求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证: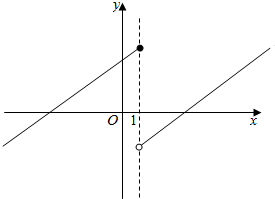 函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).
函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).