题目内容
9.已知等比数列{an}前n项和为Sn,则下列一定成立的是( )| A. | 若a7>0,则a2015<0 | B. | 若a4>0,则a2014<0 | ||
| C. | 若a7>0,则S2015>0 | D. | 若a4>0,则S2014>0 |
分析 当a7=a1q6>0时,a1>0,分当q<0时,当0<q<1时,当q>1时,和q=1时由不等式的性质可得.
解答 解:当a7=a1q6>0时,a1>0,
又当q≠1时,S2015=$\frac{{a}_{1}(1-{q}^{2015})}{1-q}$,
∴当q<0时,1-q>0,1-q2015>0,
∴$\frac{{a}_{1}(1-{q}^{2015})}{1-q}$>0,即S2015>0;
当0<q<1时,1-q>0,1-q2015>0,
∴$\frac{{a}_{1}(1-{q}^{2015})}{1-q}$>0,即S2015>0;
当q>1时,1-q<0,1-q2015<0,
∴$\frac{{a}_{1}(1-{q}^{2015})}{1-q}$>0,即S2015>0;
当q=1时,S2015=2015a7>0
综上可得当a7>0时S2015>0
故选:C.
点评 本题考查等比数列的求和公式,涉及分类讨论的思想和不等式的性质,属中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
19.已知角θ的顶点在原点,始边与x轴的正半轴重合,终边在直线2x-3y=0上,则tan2θ=( )
| A. | $\frac{12}{13}$ | B. | $\frac{12}{5}$或-$\frac{12}{5}$ | C. | $\frac{12}{5}$ | D. | -$\frac{12}{5}$或$\frac{12}{13}$ |
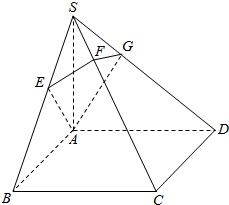 求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证:
求如图,SA⊥平面ABCD,ABCD是正方形,SC⊥平面AEFG.求证: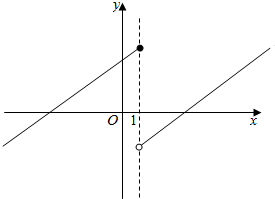 函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).
函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).