题目内容
(本小题满分12分)
用数学归纳法证明:34n+2+52n+1(n∈N)能被14整除;
用数学归纳法证明:34n+2+52n+1(n∈N)能被14整除;
①当n=0时,32+51=14,能被14整除,即当n=1时,结论成立;…………………………2分
②假设当n=k时,结论成立,即 34k+2+52k+1(k∈N)能被14整除 ……………………4分
故x=0时F(x)取得极小值为F(0)="4" ………………………………………………5分
(2)F(x)≥0恒成立 当x∈[0,+∞)时F(x)最小值≥0
①当2-a>0即a<2时由(1)知F(x)min=F(0)=4>0符合题意 ………………………7分
②若2-a≤0,即a≥2时,由(1)知x1<x2
∴当x∈[0,+∞)时,F(x)min=F[]≥0

略

练习册系列答案
相关题目
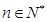 ,
,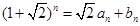 (
(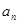 、
、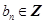 )。
)。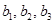 的值;
的值;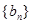 的各项均为奇数.
的各项均为奇数.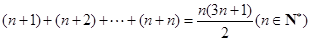
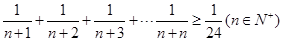 由
由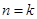 到
到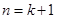 时,不等式左边应添加的项是( )
时,不等式左边应添加的项是( )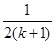
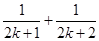
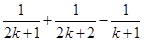
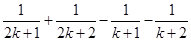
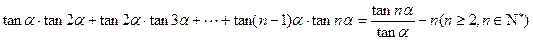
 时,
时, 成立
成立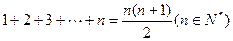 时,在验证n=1成立时,左边的项应该是
时,在验证n=1成立时,左边的项应该是  ( )
( ) 的过程中,当n=k到n=k+1时,左边所增加的项为________________
的过程中,当n=k到n=k+1时,左边所增加的项为________________