题目内容
(本题满分15分)本题理科做.
设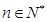 ,
,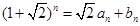 (
(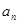 、
、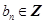 )。
)。
(1)求出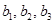 的值;
的值;
(2)求证:数列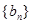 的各项均为奇数.
的各项均为奇数.
设
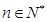 ,
,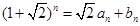 (
(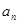 、
、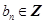 )。
)。(1)求出
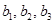 的值;
的值;(2)求证:数列
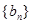 的各项均为奇数.
的各项均为奇数.(1) ,
, ,
, ;(2)见解析.
;(2)见解析.
 ,
, ,
, ;(2)见解析.
;(2)见解析.第一问利用由 ,得
,得 ,而
,而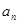 、
、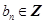
所以,只有 类似可得,
类似可得, ,
,
第二问(i)当 时,易知
时,易知 ,为奇数;
,为奇数;
(ii)假设当 时,
时, ,其中
,其中 为奇数;
为奇数;
则当 时,
时,


所以 ,
,
解(1)由 ,得
,得 ,而
,而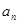 、
、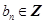
所以,只有 ,………………………2分
,………………………2分
类似可得, ,
, …………………………5分
…………………………5分
(2)证:(用数学归纳法证明)
(i)当 时,易知
时,易知 ,为奇数;……………………7分
,为奇数;……………………7分
(ii)假设当 时,
时, ,其中
,其中 为奇数;……………………8分
为奇数;……………………8分
则当 时,
时,

 ,
,
所以 , ……………………11分
, ……………………11分
又 、
、 ,所以
,所以 是偶数,
是偶数,
而由归纳假设知 是奇数,故
是奇数,故 也是奇数. ……………………14分
也是奇数. ……………………14分
综上(i)、(ii)可知, 的值一定是奇数. -----------------------------15分
的值一定是奇数. -----------------------------15分
 ,得
,得 ,而
,而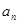 、
、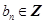
所以,只有
 类似可得,
类似可得, ,
,
第二问(i)当
 时,易知
时,易知 ,为奇数;
,为奇数; (ii)假设当
 时,
时, ,其中
,其中 为奇数;
为奇数; 则当
 时,
时,

所以
 ,
,解(1)由
 ,得
,得 ,而
,而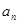 、
、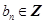
所以,只有
 ,………………………2分
,………………………2分类似可得,
 ,
, …………………………5分
…………………………5分(2)证:(用数学归纳法证明)
(i)当
 时,易知
时,易知 ,为奇数;……………………7分
,为奇数;……………………7分(ii)假设当
 时,
时, ,其中
,其中 为奇数;……………………8分
为奇数;……………………8分则当
 时,
时,
 ,
,所以
 , ……………………11分
, ……………………11分又
 、
、 ,所以
,所以 是偶数,
是偶数,而由归纳假设知
 是奇数,故
是奇数,故 也是奇数. ……………………14分
也是奇数. ……………………14分综上(i)、(ii)可知,
 的值一定是奇数. -----------------------------15分
的值一定是奇数. -----------------------------15分
练习册系列答案
相关题目
 能够被6整除.
能够被6整除.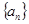 满足
满足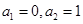 ,且对于任意的正整数
,且对于任意的正整数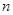 都有
都有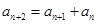 成立.
成立.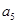 ;(2)证明:存在大于1的正整数
;(2)证明:存在大于1的正整数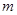 ,使得对于任意的正整数
,使得对于任意的正整数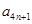 都能被
都能被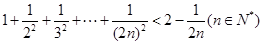 ,第二步证明“从
,第二步证明“从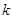 到
到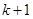 ”,左端增加的项数是( )
”,左端增加的项数是( )



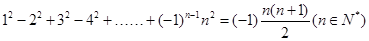 ”,
”,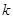 步到第
步到第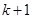 步时,左边应加上 .
步时,左边应加上 . 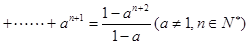 在验证n=1成立时,左边计算所得结果为 ( )
在验证n=1成立时,左边计算所得结果为 ( )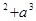
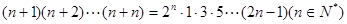 ”时,从
”时,从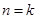 到
到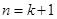 ,等式的左边需要增乘的代数式是__________ ;
,等式的左边需要增乘的代数式是__________ ;