题目内容
已知函数f(x)=x3-3ax-1,a≠0.若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,则m的取值范围是 .
(-3,1)
试题分析:因为f(x)在x=-1处取得极大值,所以f′(-1)=3×(-1)2-3a=0,∴a=1.所以f(x)=x3-3x-1,f′(x)=3x2-3,由f′(x)=0解得x1=-1,x2=1.由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.因为直线y=m与函数y=f(x)的图象有三个不同的交点,结合f(x)的单调性可知,m的取值范围是(-3,1).
点评:本题主要考查了利用导数研究函数的极值,以及求最值和利用导数研究图象等问题,属于中档题.

练习册系列答案
相关题目
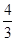 .
.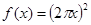 的导数是( )
的导数是( )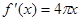
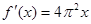
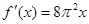
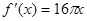
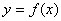 在
在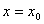 处可导,则
处可导,则 等于
等于 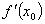
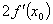
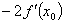
 ,若
,若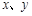 满足不等式组
满足不等式组 , 则
, 则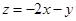 的取值范围是 .
的取值范围是 .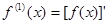 ,
,  ,…,
,…,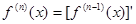
 .若
.若 ,则
,则 的值为 .
的值为 . 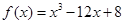 在区间
在区间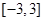 上的最大值与最小值分别为
上的最大值与最小值分别为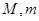 ,则
,则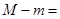 .
.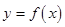 的图象在点P处的切线方程是
的图象在点P处的切线方程是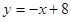 ,则
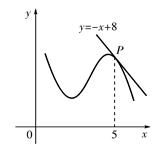
,则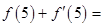 ( )
( )
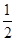
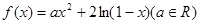 ,
, 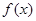 在
在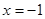 处有极值,求
处有极值,求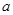 ;(2)若
;(2)若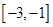 上为增函数,求
上为增函数,求