题目内容
若函数f(x)=ax3-bx+4,当x=2时,函数f(x)有极值-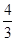 .
.
(1)求函数的解析式.
(2)若方程f(x)=k有3个不同的根,求实数k的取值范围.
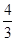 .
.(1)求函数的解析式.
(2)若方程f(x)=k有3个不同的根,求实数k的取值范围.
(1) f(x)=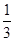 x3-4x+4.(2)-
x3-4x+4.(2)-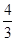 <k<
<k<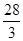 .
.
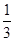 x3-4x+4.(2)-
x3-4x+4.(2)-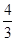 <k<
<k<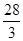 .
.试题分析:f′(x)=3ax2-b.
(1)由题意得
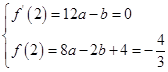 解得
解得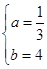
故所求函数的解析式为f(x)=
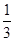 x3-4x+4.
x3-4x+4.(2)由(1)可得f′(x)=x2-4=(x-2)(x+2),
令f′(x)=0,得x=2或x=-2.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ? | 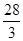 |  ? ? | -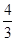 |  |
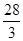 ,
,当x=2时,f(x)有极小值-
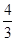 ,
,所以函数f(x)=
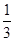 x3-4x+4的图象大致如图所示.
x3-4x+4的图象大致如图所示.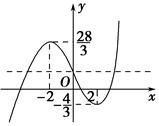
若f(x)=k有3个不同的根,则直线y=k与函数f(x)的图象有3个交点,所以-
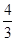 <k<
<k<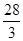 .
.点评:中档题,利用导数研究函数的单调性、极值、最值,是导数的应用中的基本问题。本题(II)应用导数,通过研究函数的单调性、极值等,对函数的图象有了充分的了解,明确了函数零点情况。

练习册系列答案
相关题目
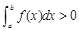 ,则f(x)>0; ⑵
,则f(x)>0; ⑵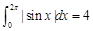 ;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则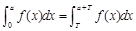 ;其中正确命题的个数为( )
;其中正确命题的个数为( )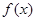 在
在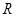 上连续可导,则
上连续可导,则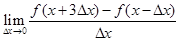 等于 ( )
等于 ( )
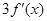
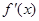
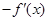
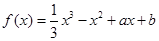 的图像在点
的图像在点 处的切线方程为
处的切线方程为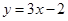 .
.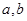 的值;
的值; 是[
是[ )上的增函数, 求实数
)上的增函数, 求实数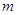 的最大值.
的最大值.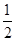 x2-2x在点
x2-2x在点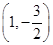 处的切线的倾斜角为( ).
处的切线的倾斜角为( ).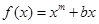 的导函数为
的导函数为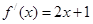 且
且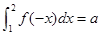 ,则
,则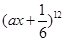 展开式中各项的系数和为
展开式中各项的系数和为
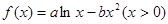 。(Ⅰ)若函数
。(Ⅰ)若函数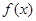 在
在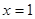 处与直线
处与直线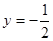 相切,①求实数
相切,①求实数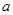 ,b的值;②求函数
,b的值;②求函数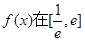 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当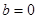 时,若不等式
时,若不等式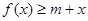 对所有的
对所有的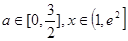 都成立,求实数m的取值范围。)
都成立,求实数m的取值范围。)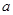 为常数,已知函数
为常数,已知函数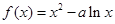 在区间
在区间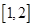 上是增函数,
上是增函数,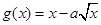 在区间
在区间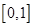 上是减函数.
上是减函数.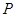 为函数
为函数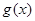 的图像上任意一点,求点
的图像上任意一点,求点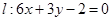 的距离的最小值;
的距离的最小值;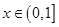 且
且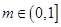 ,
,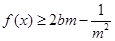 恒成立,求实数
恒成立,求实数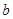 的取值范围.
的取值范围.