题目内容
 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,PD垂直底面ABCD,PD=2
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,PD垂直底面ABCD,PD=2| 2 |
| PE |
| EB |
| DF |
| FC |
(1)求BD与平面ABP所成角θ的正弦值;
(2)证明:△EFG是直角三角形;
(3)当
| PE |
| EB |
| 1 |
| 2 |
分析:(1)先证明△PAB为以∠PAB为直角的直角三角形,点D到面PAB的距离为H,由VP-ABD=VD-PAB,求出H的值,R表示,计算
sinθ=
的值.
(2)由EG∥BC,结合成比例线段,先证GF∥PD,由GF⊥BC,得 GF⊥EG,从而得到△EFG是直角三角形.
(3)根据成比例线段,求出EG和FG的值,利用△EFG的面积等于
EG•FG计算出面积.
sinθ=
| H |
| BD |
(2)由EG∥BC,结合成比例线段,先证GF∥PD,由GF⊥BC,得 GF⊥EG,从而得到△EFG是直角三角形.
(3)根据成比例线段,求出EG和FG的值,利用△EFG的面积等于
| 1 |
| 2 |
解答:解:(1)在Rt△BAD中,∵∠ABD=60°,∴AB=R,AD=
R
而PD垂直底面ABCD,
PA=
=
=
R,
PB=
=
=2
R,
在△PAB中,PA2+AB2=PB2,即△PAB为以∠PAB为直角的直角三角形.
设点D到面PAB的距离为H,由VP-ABD=VD-PAB,有PA•AB•H=AB•AD•PD,
即H=
=
=
R,sinθ=
=
.
(2)EG∥BC,∴
=
,而
=
,即
=
,
∴GF∥PD,∴GF⊥BC,∴GF⊥EG,∴△EFG是直角三角形.
(3)
=
时
=
=
,
=
=
,
即EG=
BC=
×2R×cos45°=
R,GF=
PD=
×2
R=
R,
∴△EFG的面积S△EFG=
EG•GF=
×
R×
R=
R2.
| 3 |
而PD垂直底面ABCD,
PA=
| PD2+AD2 |
(2
|
| 11 |
PB=
| PD2+BD2 |
(2
|
| 3 |
在△PAB中,PA2+AB2=PB2,即△PAB为以∠PAB为直角的直角三角形.
设点D到面PAB的距离为H,由VP-ABD=VD-PAB,有PA•AB•H=AB•AD•PD,
即H=
| AD•PD |
| PA |
| ||||
|
2
| ||
| 11 |
| H |
| BD |
| ||
| 11 |
(2)EG∥BC,∴
| PE |
| EB |
| PG |
| GC |
| PE |
| EB |
| DF |
| FC |
| PG |
| GC |
| DF |
| FC |
∴GF∥PD,∴GF⊥BC,∴GF⊥EG,∴△EFG是直角三角形.
(3)
| PE |
| EB |
| 1 |
| 2 |
| EG |
| BC |
| PE |
| PB |
| 1 |
| 3 |
| GF |
| PD |
| CF |
| CD |
| 2 |
| 3 |
即EG=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
4
| ||
| 3 |
∴△EFG的面积S△EFG=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
4
| ||
| 3 |
| 4 |
| 9 |
点评:本题考查线面成的角的求法,线面垂直的性质的应用,属于中档题.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.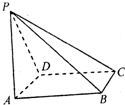 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,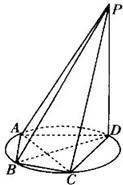 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.