题目内容
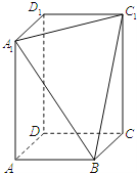
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
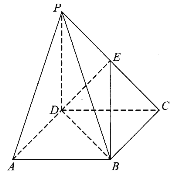
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)记阳马![]() 的体积为
的体积为![]() ,四面体
,四面体![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;四面体![]() 是鳖臑,四个面的直角分别是
是鳖臑,四个面的直角分别是![]() 、
、![]() 、
、![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则点
,则点![]() 为
为![]() 的中点,利用中位线的性质得到
的中点,利用中位线的性质得到![]() ,然后再利用直线与平面平行的判定定理可证明出
,然后再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)证明出![]() 平面
平面![]() ,可得出
,可得出![]() ,再利用三线合一的性质得出
,再利用三线合一的性质得出![]() ,再利用直线与平面垂直的判定定理可得出
,再利用直线与平面垂直的判定定理可得出![]() 平面
平面![]() ,然后结合定义判断出四面体
,然后结合定义判断出四面体![]() 是鳖臑,并写出每个面的直角;
是鳖臑,并写出每个面的直角;
(3)利用锥体的体积公式计算出![]() 和
和![]() 的表达式,即可得出
的表达式,即可得出![]() 的值.
的值.
(1)连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,则点
,则点![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,
的中点,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
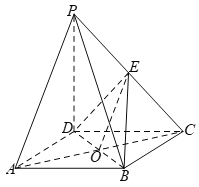
(2)因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
由底面![]() 为长方形,有
为长方形,有![]() ,而
,而![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .
.
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可知四面体
,可知四面体![]() 的四个面都是直角三角形,
的四个面都是直角三角形,
即四面体![]() 是一个鳖臑,其四个面的直角分别是
是一个鳖臑,其四个面的直角分别是![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(3)由已知,![]() 是阳马
是阳马![]() 的高,所以
的高,所以![]() ;
;
由(2)知,![]() 是鳖臑
是鳖臑![]() 的高,
的高,![]() ,
,
所以![]() .
.
在![]() 中,因为
中,因为![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
于是  .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目